本试题 “设a,b都是非零向量,命题P:a•b<0,命题Q:a与b的夹角为钝角.则P是Q的( )A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件” 主要考查您对充分条件与必要条件
用数量积表示两个向量的夹角
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 充分条件与必要条件
- 用数量积表示两个向量的夹角
1、充分条件与必要条件:一般地,“若p,则q”为真命题,是指由p通过推理可以得出q,这时,我们就说,由p可推出q,记作 ,并且说p是q的充分条件,q是p的必要条件;
,并且说p是q的充分条件,q是p的必要条件;
2、充要条件:一般地,如果既有 ,又有
,又有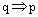 ,就记作
,就记作 ,此时,我们说,p是q的充分必要条件,简称充要条件。
,此时,我们说,p是q的充分必要条件,简称充要条件。
概括的说,如果 ,那么p与q互为充要条件。
,那么p与q互为充要条件。
3、充分不必要条件、必要不充分条件、既不充分也不必要条件:
①充分不必要条件:如果 ,且p
,且p q,则说p是q的充分不必要条件;
q,则说p是q的充分不必要条件;
②必要不充分条件:如果p q,且
q,且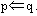 ,则说p是q的必要不充分条件;
,则说p是q的必要不充分条件;
③既不充分也不必要条件:如果p q,且p
q,且p q,则说p是q的既不充分也不必要条件。
q,则说p是q的既不充分也不必要条件。
用数量积表示两个向量的夹角:
设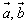 都是非零向量,
都是非零向量,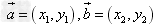 ,θ是
,θ是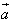 与
与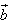 的夹角,根据向量数量积的定义及坐标表示可得
的夹角,根据向量数量积的定义及坐标表示可得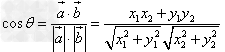 。
。
向量数量积问题中方法提炼:
(1)平面向量的数量积的运算有两种形式,一是依据定义来计算,二是利用坐标来计算,具体应用哪种形式应根据已知条件的特征来选择;
(2)平面向量数量积的计算类似于多项式的运算,解题中要注意多项式运算方法的运用;
(3)平面向量数量积的计算中要注意平面向量基本定理的应用,选择合适的基底,以简化运算
(4)向量的数量积是一个数而不是一个向量。
发现相似题
与“设a,b都是非零向量,命题P:a•b<0,命题Q:a与b的夹角为钝...”考查相似的试题有:
- 已知A,B是非空集合,命题甲:A∪B=B,命题乙:,那么[ ]A.甲是乙的充分不必要条件B.甲是乙的必要不充分条件C.甲是乙的充要条...
- 直线y=kx+1的倾斜角为钝角的一个必要非充分条件是( )A.k<0B.k<-1C.k<1D.k>-2
- 已知不等式ax2+x+c>0的解集为{x|1<x<3}.(Ⅰ)求a,c的值;(Ⅱ)若“ax2+2x+4c>0”是“x+m>0”的充分不必要条件,求实数m的...
- “a>0,b<0”是“ab<0”的( )A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件
- 已知直线l,m,n,平面α,mα,nα,则“l⊥α”是“l⊥m,且l⊥n”的( )条件.(填“充分不必要”、“必要不充分”、“充要”、“既不充分也...
- 已知是实数,则下列命题:①“”是“”的充分条件;②“”是“”的必要条件;③“”是“”的充分条件;④“”是“”的充要条件.其中是真命题的个数...
- (本小题满分12分)求至少有一个负实根的充要条件。
- 已知条件甲:函数f(x)=ax(其中a>0且a≠1)在其定义域内是减函数,条件乙:loga12>0,则条件甲是条件乙的( )A.充分而不...
- “mn>0”是“mx2+ny2=mn为椭圆”的( )条件.A.必要不充分B.充分不必要C.充要D.既不充分又不必要
- 下列说法正确的是( )A.命题“若”的逆命题是真命题B.命题“”的否定是“”C.若命题为真命题,命题为假命题,则命题“”为真命题D...