本试题 “下列说法正确的为( ).①函数y=f(x)与直线x=1的交点个数为0或l;②集合A={x|x2﹣3x﹣10≤0},B={x|a+1≤x≤2a﹣1},若BA,则﹣3≤a≤3;③函数y=f(2﹣x)与函数y=...” 主要考查您对集合间的基本关系
充分条件与必要条件
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 集合间的基本关系
- 充分条件与必要条件
集合与集合的关系有“包含”与“不包含”,“相等”三种:
1、 子集概念:
一般地,对于两个集合A与B,如果集合A的任何一个元素都是集合B的元素,就说集合B包含A,记作A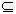 B(或说A包含于B),
B(或说A包含于B),
也可记为B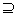 A(B包含A),此时说A是B的子集;A不是B的子集,记作A
A(B包含A),此时说A是B的子集;A不是B的子集,记作A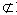 B,读作A不包含于B
B,读作A不包含于B
2、集合相等:
对于集合A和B,如果集合A中的每一个元素都是集合B的元素,反过来,集合B的每一个元素也都是集合A的元素,即集合A是集合B的子集,且集合B是集合A的子集,我么就说集合A和集合B相等,记作A=B
3、真子集:
对于集合A与B,如果A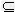 B并且A≠B,则集合A是集合B的真子集,记作A
B并且A≠B,则集合A是集合B的真子集,记作A B(B
B(B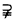 A),读作A真包含于B(B真包含A)
A),读作A真包含于B(B真包含A)
集合间基本关系:
性质1:
(1)空集是任何集合的子集,即A;
(2)空集是任何非空集合的真子集;
(3)传递性:AB,BCAC;AB,BCAC;
(4)AB,BAA=B。
性质2:
子集个数的运算:含n个元素的集合A的子集有2n个,非空子集有2n-1个,非空真子集有2n-2个。
集合间基本关系性质:
(1)空集是任何集合的子集,即A;
(2)空集是任何非空集合的真子集;
(3)传递性: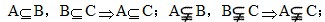
(4)集合相等:
(5)含n个元素的集合A的子集有2n个,非空子集有2n-1个,非空真子集有2n-2个。
1、充分条件与必要条件:一般地,“若p,则q”为真命题,是指由p通过推理可以得出q,这时,我们就说,由p可推出q,记作 ,并且说p是q的充分条件,q是p的必要条件;
,并且说p是q的充分条件,q是p的必要条件;
2、充要条件:一般地,如果既有 ,又有
,又有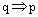 ,就记作
,就记作 ,此时,我们说,p是q的充分必要条件,简称充要条件。
,此时,我们说,p是q的充分必要条件,简称充要条件。
概括的说,如果 ,那么p与q互为充要条件。
,那么p与q互为充要条件。
3、充分不必要条件、必要不充分条件、既不充分也不必要条件:
①充分不必要条件:如果 ,且p
,且p q,则说p是q的充分不必要条件;
q,则说p是q的充分不必要条件;
②必要不充分条件:如果p q,且
q,且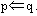 ,则说p是q的必要不充分条件;
,则说p是q的必要不充分条件;
③既不充分也不必要条件:如果p q,且p
q,且p q,则说p是q的既不充分也不必要条件。
q,则说p是q的既不充分也不必要条件。
与“下列说法正确的为( ).①函数y=f(x)与直线x=1的交点个数为0...”考查相似的试题有:
- “0<a≤15”是“函数f(x)=ax2+2(a-1)x+2在区间(-∞,4]上的减函数”的______条件.
- 一个棱柱为正四棱柱的充要条件是( )A.底面是正方形,有两个侧面垂直与底面B.底面是正方形,有两个侧面是矩形C.底面是菱...
- 已知p是r的充分条件而不必要条件,q是r的充分条件,s是r的必要条件,q是s的必要条件,现有以下命题:①s是q的充要条件;②p是q...
- 如果不等式|x-a|
- 已知集合,,则“x∈A”是“x∈B”的A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件
- 若 ,,则p是q的______________ 条件。(填“充分不必要、必要不充分、充要、既不充分也不必要”)
- 不等式x-1x>0成立的一个充分不必要条件是( )A.-1<x<0或x>1B.x<-1或0<x<1C.x>-1D.x>1
- 设x,y∈R,那么“y=logax有意义”是“y=ax有意义”的( )A.必要不充分条件B.充分不必要条件C.充分必要条件D.既不充分又不必...
- 设l,m,n均为直线,其中m,n在平面α内,“l⊥α”是“l⊥m且l⊥n”的______条件.
- 在△ABC中,“sin2A=”是“A=30°”的[ ]A、充分不必要条件B、必要不充分条件C、充要条件D、既不充分也不必要条件