本试题 “下列命题中(1)若f(x)=2cos2x2-1,则f(x+π)=f(x)对∀x∈R恒成立.(2)△ABC中,A>B是sinA>sinB的充要条件.(3)若a,b,c为非零向量,且a•b=a•c,则b=c...” 主要考查您对充分条件与必要条件
函数y=Asin(wx+φ)的图象与性质
相等向量与共线向量的定义
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 充分条件与必要条件
- 函数y=Asin(wx+φ)的图象与性质
- 相等向量与共线向量的定义
1、充分条件与必要条件:一般地,“若p,则q”为真命题,是指由p通过推理可以得出q,这时,我们就说,由p可推出q,记作 ,并且说p是q的充分条件,q是p的必要条件;
,并且说p是q的充分条件,q是p的必要条件;
2、充要条件:一般地,如果既有 ,又有
,又有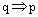 ,就记作
,就记作 ,此时,我们说,p是q的充分必要条件,简称充要条件。
,此时,我们说,p是q的充分必要条件,简称充要条件。
概括的说,如果 ,那么p与q互为充要条件。
,那么p与q互为充要条件。
3、充分不必要条件、必要不充分条件、既不充分也不必要条件:
①充分不必要条件:如果 ,且p
,且p q,则说p是q的充分不必要条件;
q,则说p是q的充分不必要条件;
②必要不充分条件:如果p q,且
q,且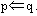 ,则说p是q的必要不充分条件;
,则说p是q的必要不充分条件;
③既不充分也不必要条件:如果p q,且p
q,且p q,则说p是q的既不充分也不必要条件。
q,则说p是q的既不充分也不必要条件。
函数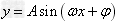 的图象:
的图象:
1、振幅、周期、频率、相位、初相:函数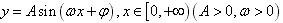 ,表示一个振动量时,A表示这个振动的振幅,往返一次所需的时间T=
,表示一个振动量时,A表示这个振动的振幅,往返一次所需的时间T=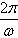 ,称为这个振动的周期,
,称为这个振动的周期,
单位时间内往返振动的次数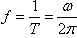 称为振动的频率,
称为振动的频率,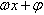 称为相位,x=0时的相位叫初相。
称为相位,x=0时的相位叫初相。
2、用“五点法”作函数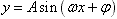 的简图主要通过变量代换,设X=
的简图主要通过变量代换,设X=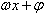 由X取0,
由X取0,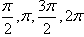 来找出相应的x的值,通过列表,计算得出五点的坐标,描点后得出图象。
来找出相应的x的值,通过列表,计算得出五点的坐标,描点后得出图象。
3、函数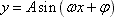 +K的图象与y=sinx的图象的关系:
+K的图象与y=sinx的图象的关系:
把y=sinx的图象纵坐标不变,横坐标向左(φ>0)或向右(φ<0), y=sin(x+φ)
y=sin(x+φ)
把y=sin(x+φ)的图象纵坐标不变,横坐标变为原来的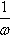 ,
, y=sin(ωx+φ)
y=sin(ωx+φ)
把y=sin(ωx+φ)的图象横坐标不变,纵坐标变为原来的A倍, y=Asin(x+φ)
y=Asin(x+φ)
把y=Asin(x+φ)的图象横坐标不变,纵坐标向上(k>0)或向下(k<0), y=Asin(x+φ)+K;
y=Asin(x+φ)+K;
若由y=sin(ωx)得到y=sin(ωx+φ)的图象,则向左或向右平移 个单位。
个单位。
函数y=Asin(x+φ)的性质:
1、y=Asin(x+φ)的周期为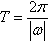 ;
;
2、y=Asin(x+φ)的的对称轴方程是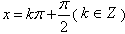 ,对称中心(kπ,0)。
,对称中心(kπ,0)。
相等向量的定义:
长度相等且方向相同的两个向量叫相等向量。
共线向量的定义:
方向相同或相反的非零向量,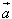 平行于
平行于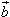 ,记作:
,记作: 。
。
规定零向量和任何向量平行。
注意:相等向量一定是共线向量,但共线向量不一定相等。表示共线向量的有向线段不一定在同一直线上,向量可以平移。
平行向量与相等向量的关系:
(l)平行向量只要求方向相同或相反即可,用有向线段表示平行向量时,向量所在的直线重合或平行.
(2)平行向量要求两个向量均为非零向量,规定:零向量与任一向量平行,记作 ;相等向量则没有这个限制,零向量与零向量相等.
;相等向量则没有这个限制,零向量与零向量相等.
(3)借助相等向量,可以把一组平行向量移动到同一直线上,因此,平行向量也叫做共线向量.(4)平行向量不一定是相等向量,但相等向量一定是平行向量.
向量共线的理解:
(1)两个非零向量平行的充要条件是这两个向量所在直线平行或重合.
(2)两个平行的非零向量在其方向与模两个要素上可能出现以下四种情况:
①方向相同,长度相同;
②方向相同,长度不同;
③方向相反,长度相同;
④方向相反,长度不同,
两个向量相等的理解:
(1)两个向量的长度相等,这两个向量不一定相等.
(2)两个向量相等,它们的起点和终点不一定相同.
(3)若a=b,b=c,则必有a=c.
与“下列命题中(1)若f(x)=2cos2x2-1,则f(x+π)=f(x)对∀x∈R...”考查相似的试题有:
- “x>2且y>2”是“x+y>4”的( )A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件
- “x>1”是“|x|>1”的( )A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分又不必要条件
- 数列的前项的和是数列成等差数列的什么条件?
- 2x2-5x-3<0的一个必要不充分条件是( ) A.-<x<3B.-<x<0C.-3<x<D.-1<x<6
- 若的必要不充分条件,则a的最小值是 .
- 已知函数的最小正周期为π,为了得到函数的图象,只要将y=f(x)的图象[ ]A.向左平移个单位长度B.向右平移个单位长度C.向左...
- 函数y=2sinx的图象按向量a平移后得到的图象的函数解析式为y=2sin(x+π3)-1,则向量a的坐标为______.
- 若函数f(x)=sin2ax-3sinaxcosax(a>0)的图象与直线y=m相切,相邻切点之间的距离为π2.(1)求m和a的值;(2)若点A(x0,...
- 函数的图象可以由y=cosx的图象[ ]A.个单位,再每点的纵坐标不变,横坐标变为原来的2倍而得B.个单位,再每点的纵坐标不变,...
- 要得到函数y=sin(2x-π5)的图象,需将函数y=sin2x的图象( )A.向左平移π10个单位B.向右平移π10个单位C.向左平移π5个单位D...