本试题 “正四棱锥V﹣ABCD的五个顶点在同一个球面上,若其底面边长为4,侧棱长为2,则[ ]A.球的表面积为18πB.AB两点的球面距为3arccosC.VA两点的球面距为3arccosD....” 主要考查您对球的表面积与体积
球面距离
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 球的表面积与体积
- 球面距离
球的体积公式:
V球=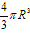 ;
;
球的表面积:
S球面=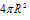
求球的表面积和体积的关键:
由球的表面积和体积公式可知,求球的表面积和体积的关键是求出半径。
常用结论:
1.若球的表面积变为原来的2倍,则半径变为原来的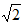 倍.
倍.
2.若球半径变为原来的2倍,则表面积变为原来的4倍.
3.若两球表面积之比为1:2,则其体积之比是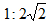 .
.
4.若两球体积之比是1:2,则其表面积之比是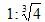 .
.
球面距离的概念:
球面上经过两点的大圆在这两点间的一段劣弧的长度,叫做这两点的球面距离。
地球上的经纬线:
①当把地球看作一个球时,经线是指球面上从北极到南极的半个大圆.纬线是指垂直于地轴的一组平行平面所截得的圆,纬线除了赤道是大圆外,其余都是小圆.如图所示.
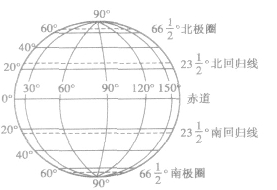
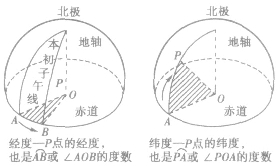
②某点的经度是经过这点的经线与地轴确定的半平面和本初子午线(00经线)与地轴确定的半平面所成的二面角度数.此角实则为二面角,某点的纬度是经过这点的球半径与赤道面所成角的度数,此角实则为线面角.下面用图标注.
对球面距离的理解:
(1)球面上的两点间的球面距离,必须是在球面过此两点的大圆中求此两点所对应的劣弧的长度,不能在过此两点的球的小圆中求.
(2)由于球是旋转体,而旋转体又是轴对称的几何体,因此在解题时,常利用球的轴截面图形来研究问题,从而将空间问题转化为平面问题.
(3)熟练掌握球的截面中大圆的半径,截面圆半径以及球心到截面圆圆心的距离的关系是解决有关球的问题的关键.
发现相似题
与“正四棱锥V﹣ABCD的五个顶点在同一个球面上,若其底面边长为4...”考查相似的试题有:
- 球面上有A,B,C三点,AB=23,BC=26,CA=6,若球心到平面ABC的距离为4,则球的表面积为______.
- 将棱长为1的正方体木块切削成一个体积最大的球,则该球的体积为( ) A. B. C. D.
- 轴截面是正方形的圆柱的侧面积是S,则与它的体积相等的球的表面积是 ______.
- 在四棱锥P -ABCD中,底面是边长为2的菱形,∠DAB=60°,对角线AC与BD交于点O,PO⊥平面ABCD,PB与平面ABCD所成角为60°.(1)求四棱锥的...
- 如图,长方体中,为线段的中点,.(Ⅰ)证明:⊥平面;(Ⅱ)求点到平面的距离.
- 在棱长为1的正方体上,分别用过共顶点的三条棱中点的平面截该正方体,则截去8个三棱锥后 ,剩下的几何体的体积是________
- 若正三棱锥底面边长为1,侧棱与底面所成的角为,则其体积为____________。
- 已知一个球与一个二面角的两个半平面都相切,若球心到二面角的棱的距离是5,切点到二面角棱的距离是1,则球的表面积是______...
- 菱形中,,且,现将三角形沿着折起形成四面体,如图所示.(1)当为多大时,面?并证明;(2)在(1)的条件下,求点到面的距离.
- 如图所示,正方体ABCDA1B1C1D1的棱长为6,则以正方体ABCDA1B1C1D1的中心为顶点,以平面AB1D1截正方体外接球所得的圆为底面的...