本试题 “求适合下列条件的圆锥曲线的标准方程:(1)中心在原点,焦点在 x轴上,短轴长为12,离心率为45的椭圆;(2)抛物线的顶点在原点,它的准线过双曲线x2a2-y2b2...” 主要考查您对椭圆的标准方程及图象
双曲线的标准方程及图象
抛物线的标准方程及图象
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 椭圆的标准方程及图象
- 双曲线的标准方程及图象
- 抛物线的标准方程及图象
椭圆的标准方程:
(1)中心在原点,焦点在x轴上: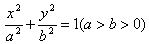 ;
;
(2)中心在原点,焦点在y轴上: 。
。
椭圆的图像:
(1)焦点在x轴: ;
;
(2)焦点在y轴: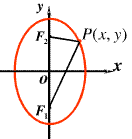 。
。
巧记椭圆标准方程的形式:
①椭圆标准方程的形式:左边是两个分式的平方和,右边是1;
②椭圆的标准方程中,x2与y2的分母哪一个大,则焦点在哪一个轴上;
③椭圆的标准方程中,三个参数a,b,c满足a2= b2+ c2;
④由椭圆的标准方程可以求出三个参数a,b,c的值.
待定系数法求椭圆的标准方程:
求椭圆的标准方程常用待定系数法,要恰当地选择方程的形式,如果不能确定焦点的位置,那么有两种方法来解决问题:一是分类讨论,全面考虑问题;二是可把椭圆的方程设为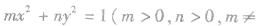 n)用待定系数法求出m,n的值,从而求出标准方程,
n)用待定系数法求出m,n的值,从而求出标准方程,
双曲线的标准方程:
(1)中心在原点,焦点在x轴上: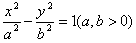 ;
;
(2)中心在原点,焦点在y轴上: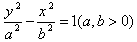 。
。
双曲线的图像:
(1)焦点在x轴上的双曲线的图像 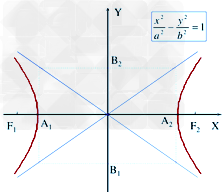 ;
;
(2)焦点在y轴上的双曲线的图像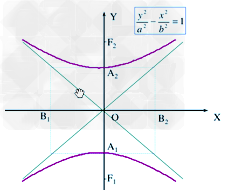 。
。
判断双曲线的焦点在哪个轴上:
判断双曲线的焦点在哪个轴上的方法看未知数前的系数,哪一个为正,焦点就在哪一个轴上.
定义法求双曲线的标准方程:
求动点的轨迹方程时,可利用定义先判断动点的轨迹,再写出方程.平面几何中的定理性质在解决解析几何问题时起着简化运算的作用,一定要注意应用,根据双曲线的定义,到两个定点的距离之差的绝对值是一个常数的点的轨迹是双曲线,可以求双曲线的标准方程,
待定系数法求双曲线的标准方程:
在求双曲线标准方程时,可先设出其标准方程,再根据双曲线的参数a,b,c,e的取值及相互之间的关系,求出a,b的值,已知双曲线的渐近线方程,求双曲线方程时,可利用共渐近线双曲线系方程 ,再由其他条件求λ.若焦点不确定时,要注意分类讨论.
,再由其他条件求λ.若焦点不确定时,要注意分类讨论.
利用双曲线的性质求解有关问题:
要解决双曲线中有关求离心率或求离心率范围的问题,应找好题中的等量关系或不等关系,构造出离心率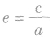 的关系式,这里应和椭圆中a,b,c的关系区分好,即
的关系式,这里应和椭圆中a,b,c的关系区分好,即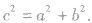
几种特殊的双曲线:
| 等轴双曲线 | 实轴和虚轴相等的双曲线叫做等轴双曲线.离心率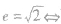 两条渐近线互相垂直 两条渐近线互相垂直 |
| 共轭双曲线 |
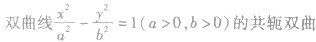
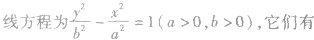

 |
| 共渐近线的双曲线 |

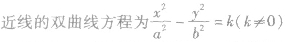 |
抛物线的标准方程及图像(见下表):

抛物线的标准方程的理解:
①抛物线的标准方程是指抛物线在标准状态下的方程,即顶点在原点,焦点在坐标轴上;
②抛物线的标准方程中的系数p叫做焦参数,它的几何意义是:焦点到准线的距离.焦点到顶点以及顶点到准线的距离均为
③抛物线的标准方程有四种类型,所以判断其类型是解题的关键,在方程的类型已确定的前提下,由于标准方程只有一个参数p,所以只需一个条件就可以确定一个抛物线的方程;
④对以上四种位置不同的抛物线和它们的标准方程进行对比、分析,得出其异同点。
共同点:
a.原点在抛物线上;
b.焦点都在坐标轴上;
c.准线与焦点所在轴垂直,垂足与焦点分别关于原点对称,它们与原点的距离都等于一次项系数的绝对值的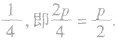
不同点:
a.焦点在x轴上时,方程的右侧为±2px,左端为y2;焦点在y轴上时,方程的右端为±2py,左端为x2;
b.开口方向与x轴(或y轴)的正半轴相同,焦点在x轴(或y轴)的正半轴上,方程右端取正号;开口方向与x轴(或y轴)的负半轴相同,焦点在x轴(或y轴)的负半轴上,方程的右端取负号.
求抛物线的标准方程的常用方法:
(1)定义法求抛物线的标准方程:定义法求曲线方程是经常用的一种方法,关键是理解定义的实质及注意条件,将所给条件转化为定义的条件,当然还应注意特殊情况.
(2)待定系数法求抛物线的标准方程:求抛物线标准方程常用的方法是待定系数法,为避免开口不确定,分成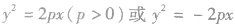 (p>0)两种情况求解的麻烦,可以设成
(p>0)两种情况求解的麻烦,可以设成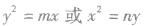 (m,n≠0),若m、n>0,开口向右或向上;m、n<0,开口向左或向下;m、n有两解,则抛物线的标准方程各有两个。
(m,n≠0),若m、n>0,开口向右或向上;m、n<0,开口向左或向下;m、n有两解,则抛物线的标准方程各有两个。
与“求适合下列条件的圆锥曲线的标准方程:(1)中心在原点,焦点...”考查相似的试题有:
- 已知以原点为对称中心、F(2,0)为右焦点的椭圆C过P(2,2),直线l:y=kx+m(k≠0)交椭圆C于不同的两点A,B.(Ⅰ)求椭圆C...
- 已知椭圆的焦点为F1(-1,0)和F2(1,0),点P是椭圆上的一点,且|F1F2|是|PF1|和|PF2|的等差中项,则该椭圆的方程为[ ]A.B....
- 已知点P为圆x2+y2=4上的动点,且P不在x轴上,PD⊥x轴,垂足为D,线段PD中点Q的轨迹为曲线C,过定点M(t,0)(0<t<2)任作一...
- 已知椭圆的中心在原点,一个焦点是F(2,0),且两条准线间的距离为λ(λ>4).(I)求椭圆的方程;(II)若存在过点A(1,0...
- 椭圆(a>b>0)与x,y轴的正半轴分别交于A,B两点,原点O到直线AB的距离为,该椭圆的离心率为(Ⅰ)求椭圆的方程;(Ⅱ)是否存...
- 已知方程(1+k)x2-(1-k)y2=1表示焦点在x轴上的双曲线,则k的取值范围为( ) A.-1<k<1 B.k>1 C.k<-1 D.k>1或k<-1
- 已知双曲线C与双曲线x216-y29=1有共同的渐近线,且经过点P(4,-32).(I)求双曲线C的方程及其准线方程;(Ⅱ)若直线y=kx+1与...
- 抛物线y=ax2(a≠0)的焦点坐标是( ) A.(,0) B.(-,0) C.(0,-) D.(0,)
- 设抛物线的顶点在原点,准线方程为x=-2,则抛物线的方程是A、y2=-8xB、y2=8xC、y2=-4xD、y2=4x
- 对抛物线x2=-4y,下列描述正确的是( ) A.开口向下,焦点为(0,-) B.开口向下,焦点为(0,-1) C.开口向左,焦点为(-...