本试题 “在△ABC中,AB=2,BC=1,cosC=34.(Ⅰ)求sinA的值;(Ⅱ)求BC•CA的值.” 主要考查您对正弦定理
向量数量积的运算
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 正弦定理
- 向量数量积的运算
正弦定理:
在一个三角形中,各边和它所对角的正弦的比相等,即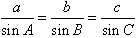 =2R。
=2R。
有以下一些变式:
(1)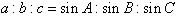 ;
;
(2)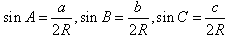 ;
;
(3)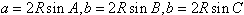 。
。
正弦定理在解三角形中的应用:
(1)已知两角和一边解三角形,只有一解。
(2)已知两边和其中一边的对角,解三角形,要注意对解的个数的讨论。可按如下步骤和方法进行:先看已知角的性质和已知两边的大小关系。
如已知a,b,A,
(一)若A为钝角或直角,当b≥a时,则无解;当a≥b时,有只有一个解;
(二)若A为锐角,结合下图理解。
①若a≥b或a=bsinA,则只有一个解。
②若bsinA<a<b,则有两解。
③若a<bsinA,则无解。 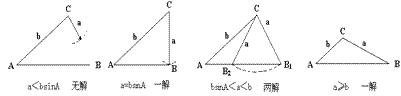
也可根据a,b的关系及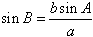 与1的大小关系来确定。
与1的大小关系来确定。
两个向量数量积的含义:
如果两个非零向量 ,
, ,它们的夹角为
,它们的夹角为 ,我们把数量
,我们把数量 叫做
叫做 与
与 的数量积(或内积或点积),记作:
的数量积(或内积或点积),记作: ,即
,即 。
。 叫
叫 在
在 上的投影。
上的投影。
规定:零向量与任一向量的数量积是0,注意数量积是一个实数,不再是一个向量。
数量积的的运算律:
已知向量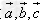 和实数λ,下面(1)(2)(3)分别叫做交换律,数乘结合律,分配律。
和实数λ,下面(1)(2)(3)分别叫做交换律,数乘结合律,分配律。
(1)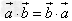 ;
;
(2)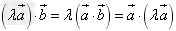 ;
;
(3)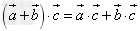 。
。
向量数量积的性质:
设两个非零向量
(1) ;
;
(2) ;
;
(3) ;
;
(4) ;
;
(5)当 ,
, 同向时,
同向时, ;当
;当 与
与 反向时,
反向时, ;当
;当 为锐角时,
为锐角时, 为正且
为正且 ,
, 不同向,
不同向, ;当
;当 为钝角时,
为钝角时, 为负且
为负且 ,
, 不反向,
不反向, 。
。
发现相似题
与“在△ABC中,AB=2,BC=1,cosC=34.(Ⅰ)求sinA的值;(Ⅱ)求BC...”考查相似的试题有:
- 在△ABC中,已知a=52,c=10,A=30°,则B等于( )A.105°B.60°C.15°D.105°或15°
- (本小题满分12分) 在中,角A、B、C所对边分别是a、b、c,,求.
- 看下图回答问题
- 在△ABC中,角A,B,C的对边分别为a,b,c,且A,B,C成等差数列.(1)若b=23,c=2,求△ABC的面积;(2)若sinA,sinB,sinC...
- 在△ABC中,AB=2,BC=1,cosC=34,(1)则sinA=______;(2)BC•CA=______.
- 已知m=(cosϖx,sinϖx),n=(cosϖx,23cosϖx-sinϖx),ϖ>0,函数f(x)=m•n+|m|,x1,x2是集合M={x|f(x)=1}中任意两个元素,且|...
- 已知函数,x∈R,将函数f(x)向左平移个单位后得函数g(x),设△ABC三个角A、B、C的对边分别为a、b、c.(Ⅰ)若,f(C)=0,s...
- 下列命题中的真命题是( )A.AB-AC=BCB.若a•b=0,则a=0或b=0C.(a•b)•c=a•(b•c)D.若|a| > |b|,则a2>b2
- 在锐角△ABC中,三个内角A,B,C所对的边依次为a,b,c,设m=(sin(π4-A),1),n=(2sin(π4+1),-1),a=23,且m•n=-32....
- 己知正方形ABCD的边长为1,点E是AB边上的动点.则的值为( )。