本试题 “求证:x>1时,2x3>x2+1.” 主要考查您对函数的最值与导数的关系
综合法与分析法
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 函数的最值与导数的关系
- 综合法与分析法
函数的最大值和最小值:
在闭区间[a,b]上连续的函数f(x)在[a,b]上必有最大值与最小值,分别对应该区间上的函数值的最大值和最小值。
利用导数求函数的最值步骤:
(1)求f(x)在(a,b)内的极值;
(2)将f(x)的各极值与f(a)、f(b)比较得出函数f(x)在[a,b]上的最值。
用导数的方法求最值特别提醒:
①求函数的最大值和最小值需先确定函数的极大值和极小值,因此,函数极大值和极小值的判别是关键,极值与最值的关系:极大(小)值不一定是最大(小)值,最大(小)值也不一定是极大(小)值;
②如果仅仅是求最值,还可将上面的办法化简,因为函数fx在[a,b]内的全部极值,只能在f(x)的导数为零的点或导数不存在的点取得(下称这两种点为可疑点),所以只需要将这些可疑点求出来,然后算出f(x)在可疑点处的函数值,与区间端点处的函数值进行比较,就能求得最大值和最小值;
③当f(x)为连续函数且在[a,b]上单调时,其最大值、最小值在端点处取得。
生活中的优化问题:
生活中经常遇到求利润最大、用料最省、效率最高等问题,这些问题通常称为优化问题,解决优化问题的方法很多,如:判别式法,均值不等式法,线性规划及利用二次函数的性质等,
不少优化问题可以化为求函数最值问题.导数方法是解这类问题的有效工具.
用导数解决生活中的优化问题应当注意的问题:
(1)在求实际问题的最大(小)值时,一定要考虑实际问题的意义,不符合实际意义的值应舍去;
(2)在实际问题中,有时会遇到函数在区间内只有一个点使f'(x)=0的情形.如果函数在这点有极大(小)值,那么不与端点比较,也可以知道这就是最大(小)值;
(3)在解决实际优化问题时,不仅要注意将问题中涉及的变量关系用函数关系表示,还应确定出函数关系式中自变量的定义区间.
利用导数解决生活中的优化问题:
(1)运用导数解决实际问题,关键是要建立恰当的数学模型(函数关系、方程或不等式),运用导数的知识与方法去解决,主要是转化为求最值问题,最后反馈到实际问题之中.
(2)利用导数求f(x)在闭区间[a,b]上的最大值和最小值的步骤,
①求函数y =f(x)在(a,b)上的极值;
②将函数y=f(x)的各极值与端点处的函数值f(a)、f(b)比较,其中最大的一个是最大值,最小的一个是最小值.
(3)定义在开区间(a,b)上的可导函数,如果只有一个极值点,该极值点必为最值点.
综合法:
一般地,利用已知条件和某些数学定义、公理、定理等,经过一系列的推理论证,最后推导出所要证明的结论成立,这种证明方法叫做综合法。
图解: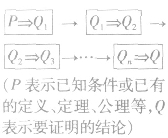
分析法:
一般地,从要证明的结论出发,逐步寻求使它成立的充分条件,直到最后,把要证明的结论归结为判定一个明显成立的条件(已知条件、定理、定义、公理等)为止,这种证明方法叫做分析法。
图解: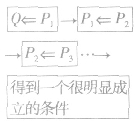
分析法的思维特点:
执果索因;分析法的书写格式:要证明命题B为真,只需要证明命题为真,从而有……,这只需要证明命题为真,从而又有…… 这只需要证明命题A为真,而已知A为真,故命题B必为真。
分析法与综合法综合:
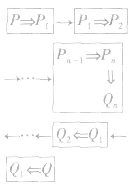
综合法的思维方法:
综合法的思维方向是”,即由已知条件出发,逐步推出其必要条件(由因导果),最后推导出所要证明的结论成立,故综合法又叫顺推证法或由因导果法.综合法的依据:已知条件以及逻辑推理的基本理论,在推理时要注意:作为依据和出发点的命题一定要正确.
分析法的思维方向:
分析法的思维方向是”,即由待证的结论出发,逐步逆求它要成立的充分条件(执果索因),最后得到的充分条件是已知(或已证)的命题,故分析法又叫逆推证法或执果索因法.
用分析法证明的模式:
用分析法证:为了证明命题B为真,这只需证明命题B,为真,从而有……这只需证明命题B:为真,从而有……这只需证明命题A为真.而已知A为真,故B必真.可见分析法是”,步步寻求上一步成立的充分条件,它与综合法是对立统一的两种方法。
特别提醒:当命题不知从何人手时,有时可以运用分析法来解决,特别是对于条件简单而结论复杂的题目,往往更是行之有效.用分析法证明时,往往在最后加上一句步可逆,这无形中就出现了两个问题:①分析法证明过程的每一步不一定”,也没有必要要求”,因为这时仅需寻找充分条件,而不是充要条件;②如果非要”,则限制了分析法解决问题的范围,使得分析法只适用于证明等价命题了,但是,只要我们搞清了用分析法证明问题的逻辑结构,明确四种命题之间的关系,那么用分析法证明不等式还是比较方便的。
与“求证:x>1时,2x3>x2+1.”考查相似的试题有:
- 已知函数f(x)=lnxa-x.(Ⅰ)若曲线y=f(x)在点(1,f(1))处的切线与X轴平行,求函数f(x)的单调区间;(Ⅱ)若对一切正...
- 已知a是实数,函数。(I)求函数f(x)的单调区间;(II)设g(a)为f(x)在区间[0,2]上的最小值。(i)写出g(a)的表达式...
- 已知函数f(x)=ax3+bx2﹣3x(a,b∈R)在点(1,f(1))处的切线方程为y+2=0.(1)求函数f(x)的解析式;(2)若对于区间[...
- 若a1x≤sinx≤a2x对任意的x∈[0,π2]都成立,则a2-a1的最小值为______.
- 已知函数f(x)=x2-2elnx,求函数f(x)的单调区间和最值。
- f(x)=2x3﹣6x2+a在[﹣2,2]上有最大值3,那么在[﹣2,2]上f(x)的最小值是[ ]A.﹣5B.﹣11C.﹣29D.﹣37
- 已知函数f(x)=1x+alnx(a≠0,a∈R)(Ⅰ)若a=1,求函数f(x)的极值和单调区间;(II)若在区间[1,e]上至少存在一点x0,使得f(...
- 已知函数.(1)当时,求曲线在点的切线方程;(2)对一切,恒成立,求实数的取值范围;(3)当时,试讨论在内的极值点的个数.
- 已知函数f(x)=ax3-2bx2+cx(a,b,c∈R)的图象关于原点对称,且当x=1时,f(x)取得极值-23.(Ⅰ)求a,b,c的值;(Ⅱ)若...
- (本小题满分14分)给定函数(1)试求函数的单调减区间;(2)已知各项均为负的数列满足,求证:;(3)设,为数列的前项和,...