本试题 “在直角坐标系xOy中,i,j分别是与x轴,y轴平行的单位向量,若在Rt△ABC中,AB=i+j,AC=2i+mj,则实数m=______.” 主要考查您对零向量与单位向量
平面向量基本定理及坐标表示
向量数量积的运算
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 零向量与单位向量
- 平面向量基本定理及坐标表示
- 向量数量积的运算
零向量的定义:
长度为0的向量叫零向量,记作: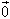 ,注意零向量的方向是任意的。
,注意零向量的方向是任意的。
单位向量的定义:
长度为一个单位长度的向量叫做单位向量,常用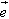 表示。
表示。
零向量和单位向量的理解:
(1)注意零向量与数零的含义与书写的区别,零向量是一个向量所以零向量是有方向的并且规定零向量的方向是任意的;
(2)零向量和单位向量的定义都只是限制了大小;
(3)所有的单位向量都是相等向量是一种错误的说法,因为它们的方向可能不同;所有单位向量的模都相等是一种正确的说法,并且它们的模都等于1.
平面向量的基本定理:
如果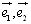 是同一平面内的两个不共线的向量,那么对这一平面内的任一向量
是同一平面内的两个不共线的向量,那么对这一平面内的任一向量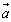 存在唯一的一对有序实数
存在唯一的一对有序实数 使
使 成立,不共线向量
成立,不共线向量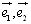 表示这一平面内所有向量的一组基底。
表示这一平面内所有向量的一组基底。
平面向量的坐标运算:
在平面内建立直角坐标系,以与x轴、y轴方向相同的两个单位向量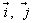 为基底,则平面内的任一向量
为基底,则平面内的任一向量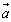 可表示为
可表示为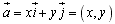 ,称(x,y)为向量
,称(x,y)为向量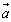 的坐标,
的坐标,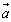 =(x,y)叫做向量
=(x,y)叫做向量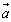 的坐标表示。
的坐标表示。
基底在向量中的应用:
(l)用基底表示出相关向量来解决向量问题是常用的方法之一.
(2)在平面中选择基底主要有以下几个特点:①不共线;②有公共起点;③其长度及两两夹角已知.(3)用基底表示向量,就是利用向量的加法和减法对有关向量进行分解。
用已知向量表示未知向量:
用已知向量表示未知向量,一定要结合图像,可从以下角度如手:
(1)要用基向量意识,把有关向量尽量统一到基向量上来;
(2)把要表示的向量标在封闭的图形中,表示为其它向量的和或差的形式,进而寻找这些向量与基向量的关系;
(3)用基向量表示一个向量时,如果此向量的起点是从基底的公共点出发的,一般考虑用加法,否则用减法,如果此向量与一个易求向量共线,可用数乘。
两个向量数量积的含义:
如果两个非零向量 ,
, ,它们的夹角为
,它们的夹角为 ,我们把数量
,我们把数量 叫做
叫做 与
与 的数量积(或内积或点积),记作:
的数量积(或内积或点积),记作: ,即
,即 。
。 叫
叫 在
在 上的投影。
上的投影。
规定:零向量与任一向量的数量积是0,注意数量积是一个实数,不再是一个向量。
数量积的的运算律:
已知向量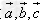 和实数λ,下面(1)(2)(3)分别叫做交换律,数乘结合律,分配律。
和实数λ,下面(1)(2)(3)分别叫做交换律,数乘结合律,分配律。
(1)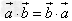 ;
;
(2)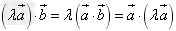 ;
;
(3)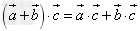 。
。
向量数量积的性质:
设两个非零向量
(1) ;
;
(2) ;
;
(3) ;
;
(4) ;
;
(5)当 ,
, 同向时,
同向时, ;当
;当 与
与 反向时,
反向时, ;当
;当 为锐角时,
为锐角时, 为正且
为正且 ,
, 不同向,
不同向, ;当
;当 为钝角时,
为钝角时, 为负且
为负且 ,
, 不反向,
不反向, 。
。
与“在直角坐标系xOy中,i,j分别是与x轴,y轴平行的单位向量,若...”考查相似的试题有:
- 已知平面向量a=(-1,2),b=(2,y),且a∥b,则3a+2b=( )A.(-1,7)B.(-1,2)C.(1,2)D.(1,-2)
- 已知向量a=(1,3),则与向量a平行的一个单位向量是______.
- 已知点A(1,0),B(0,1),C(2sinθ,cosθ).(1)若|AC|=|BC|,求tanθ的值;(2)若(OA+2OB)•OC=1,其中O为坐标原点,求...
- 已知向量a=(2,4),b=(1,1),c=(12,52),若c=λa+μb,则λ+μ=______.
- 如图,、分别是射线上的两点,给出下列向量:①;②;③; ④;⑤.这些向量中以为起点,终点在阴影区域内的是( )A.①②B.①④C.①③D.⑤
- 已知M(1+cos2x,1),N(1,3sin2x+a)(x∈R,a∈R,a是常数),且y=OM•ON(其中O为坐标原点).(1)求y关于x的函数关系式y=f...
- 若a、b、c为任意向量,m∈R,则下列等式不一定成立的是( )A.(a+b)+c=a+(b+c)B.(a+b)•c=a•c+b•cC.m(a+b)=ma+mbD....
- 在平面直角坐标系中,O为坐标原点,已知向量a=(-1,2),又点A(8,0),B(n,t),C(ksinθ,t).(1)若AB⊥a,且|AB|=5|OA...
- (Ⅰ)①证明两角和的余弦公式C(α+β):cos(α+β)=cosαcosβ-sinαsinβ;②由C(α+β)推导两角和的正弦公式S(α+β):sin(α+β)=sinαcosβ+co...
- 已知a=(a1,a2),b=(b1,b2),丨a丨=5,丨b丨=6,a•b=30,则a1+a2b1+b2=______.