椭圆的标准方程：
（1）中心在原点，焦点在x轴上：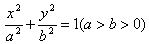
；
（2）中心在原点，焦点在y轴上：
。
椭圆的图像：
（1）焦点在x轴：
；
（2）焦点在y轴：
。
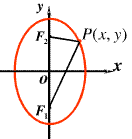巧记椭圆标准方程的形式：
①椭圆标准方程的形式：左边是两个分式的平方和，右边是1；
②椭圆的标准方程中，x2与y2的分母哪一个大，则焦点在哪一个轴上；
③椭圆的标准方程中，三个参数a，b，c满足a2= b2+ c2；
④由椭圆的标准方程可以求出三个参数a，b，c的值．
待定系数法求椭圆的标准方程：
求椭圆的标准方程常用待定系数法，要恰当地选择方程的形式，如果不能确定焦点的位置，那么有两种方法来解决问题：一是分类讨论，全面考虑问题；二是可把椭圆的方程设为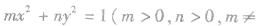
n)用待定系数法求出m，n的值，从而求出标准方程，
抛物线的性质（见下表）:
抛物线的焦点弦的性质：
关于抛物线的几个重要结论：
(1)弦长公式同椭圆．
(2)对于抛物线y2=2px(p>0)，我们有P(x0，y0)在抛物线内部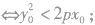
P(x0，y0)在抛物线外部
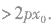
(3)抛物线y2=2px上的点P（x1，y1）的切线方程是
抛物线y2=2px(p>0)的斜率为k的切线方程是y=kx+
(4)抛物线y2=2px外一点P(x0，y0)的切点弦方程是
(5)过抛物线y2=2px上两点
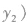的两条切线交于点M(x0，y0)，则
(6)自抛物线外一点P作两条切线，切点为A,B，若焦点为F,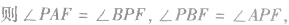
又若切线PA⊥PB，则AB必过抛物线焦点F．
利用抛物线的几何性质解题的方法：
根据抛物线定义得出抛物线一个非常重要的几何性质：抛物线上的点到焦点的距离等于到准线的距离．利用抛物线的几何性质，可以进行求值、图形的判断及有关证明．
抛物线中定点问题的解决方法：
在高考中一般以填空题或选择题的形式考查抛物线的定义、标准方程以及几何性质等基础知识，在解答题中常常将解析几何中的方法、技巧与思想集于一身，与其他圆锥曲线或其他章节的内容相结合，考查综合分析问题的能力，而与抛物线有关的定值及最值问题是一个很好的切人点，充分利用点在抛物线上及抛物线方程的特点是解决此类题型的关键，在求最值时经常运用基本不等式、判别式以及转化为函数最值等方法。
利用焦点弦求值：
利用抛物线及焦半径的定义，结合焦点弦的表示，进行有关的计算或求值。
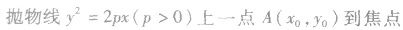
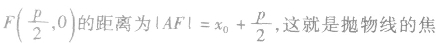
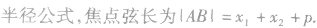
抛物线中的几何证明方法：
利用抛物线的定义及几何性质、焦点弦等进行有关的几何证明是抛物线中的一种常见题型，证明时注意利用好图形，并做好转化代换。
圆锥曲线的综合问题：
1、圆锥曲线的范围问题有两种常用方法：
（1）寻找合理的不等式，常见有△＞0和弦的中点在曲线内部；
（2）所求量可表示为另一变量的函数，求函数的值域。
2、圆锥曲线的最值、定值及过定点等难点问题。
直线与圆锥曲线的位置关系：
(1)从几何角度来看，直线和圆锥曲线有三种位置关系：相离、相切和相交，相离是直线和圆锥曲线没有公共点，相切是直线和圆锥曲线有唯一公共点，相交是直线与圆锥曲线有两个不同的公共点，并特别注意直线与双曲线、抛物线有唯一公共点时，并不一定是相切，如直线与双曲线的渐近线平行时，与双曲线有唯一公共点，但这时直线与双曲线相交；直线平行（重合）于抛物线的对称轴时，与抛物线有唯一公共点，但这时直线与抛物线相交，故直线与双曲线、抛物线有唯一公共点时可能是相切，也可能是相交，直线与这两种曲线相交，可能有两个交点，也可能有一个交点，从而不要以公共点的个数来判断直线与曲线的位置关系，但由位置关系可以确定公共点的个数．
(2)从代数角度来看，可以根据直线方程和圆锥曲线方程组成的方程组解的个数确定位置关系．设直线l的方程与圆锥曲线方程联立得到ax2+bx+c=0．
①若a=0，当圆锥曲线是双曲线时，直线l与双曲线的渐近线平行或重合；当圆锥曲线是抛物线时，直线l与抛物线的对称轴平行或重合．
②若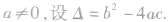
当Δ>0时，直线和圆锥曲线相交于不同两点，相交．
当Δ=0时，直线和圆锥曲线相切于一点，相切．
当Δ<0时，直线和圆锥曲线没有公共点，相离．
直线与圆锥曲线相交的弦长公式：
若直线l与圆锥曲线F(x，y)=0相交于A，B两点，求弦AB的长可用下列两种方法：
(1)求交点法：把直线的方程与圆锥曲线的方程联立，解得点A，B的坐标，然后用两点间距离公式，便得到弦AB的长，一般来说，这种方法较为麻烦．
(2)韦达定理法：
不求交点坐标，可用韦达定理求解．若直线l的方程用y=kx+m或x=n表示．
