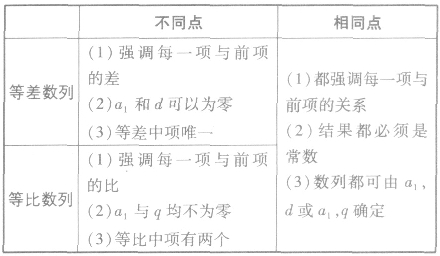
本试题 “若x、y∈R,且2y是1+x和1-x的等比中项,则动点(x,y)的轨迹为除去x轴上点的( )A.一条直线B.一个圆C.双曲线的一支D.一个椭圆” 主要考查您对等比数列的定义及性质
动点的轨迹方程
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 等比数列的定义及性质
- 动点的轨迹方程
等比数列的定义:
一般地,如果一个数列从第2项起,每一项与它的前一项的比等于同一个常数,那么这个数列就叫做等比数列,这个常数叫做公比,公比通常用字母q表示(q≠0)。
等比数列的性质:
在等比数列{an}中,有
(1)若m+n=p+q,m,n,p,q∈N*,则aman=apaq;当m+n=2p时,aman=ap2;
(2)若m,n∈N*,则am=anqm-n;
(3)若公比为q,则{ }是以
}是以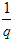 为公比的等比数列;
为公比的等比数列;
(4)下标成等差数列的项构成等比数列;
(5)
1)若a1>0,q>1,则{an}为递增数列;
2)a1<0,q>1, 则{an}为递减数列;
3)a1>0,0<q<1,则{an}为递减数列;
4)a1<0, 0<q<1, 则{an}为递增数列;
5)q<0,则{an}为摆动数列;若q=1,则{an}为常数列。
如何证明一个数列是等比数列:
证明一个数列是等比数列,只需证明 是一个与n无关的常数即可(或an2=an-1an+1)。
是一个与n无关的常数即可(或an2=an-1an+1)。
动点的轨迹方程:
在直角坐标系中,动点所经过的轨迹用一个二元方程f(x,y)=0表示出来。
求动点的轨迹方程的基本方法:
直接法、定义法、相关点法、参数法、交轨法等。
1、直接法:
如果动点运动的条件就是一些几何量的等量关系,这些条件简单明确,不需要特殊的技巧,易于表述成含x,y的等式,就得到轨迹方程,这种方法称之为直接法;
用直接法求动点轨迹一般有建系,设点,列式,化简,证明五个步骤,最后的证明可以省略,但要注意“挖”与“补”。求轨迹方程一般只要求出方程即可,求轨迹却不仅要求出方程而且要说明轨迹是什么。
2、定义法:
利用所学过的圆的定义、椭圆的定义、双曲线的定义、抛物线的定义直接写出所求的动点的轨迹方程,这种方法叫做定义法.这种方法要求题设中有定点与定直线及两定点距离之和或差为定值的条件,或利用平面几何知识分析得出这些条件。定义法的关键是条件的转化——转化成某一基本轨迹的定义条件;
3、相关点法:
动点所满足的条件不易表述或求出,但形成轨迹的动点P(x,y)却随另一动点Q(x′,y′)的运动而有规律的运动,且动点Q的轨迹为给定或容易求得,则可先将x′,y′表示为x,y的式子,再代入Q的轨迹方程,然而整理得P的轨迹方程,代入法也称相关点法。一般地:定比分点问题,对称问题或能转化为这两类的轨迹问题,都可用相关点法。
4、参数法:
求轨迹方程有时很难直接找到动点的横坐标、纵坐标之间的关系,则可借助中间变量(参数),使x,y之间建立起联系,然而再从所求式子中消去参数,得出动点的轨迹方程。用什么变量为参数,要看动点随什么量的变化而变化,常见的参数有:斜率、截距、定比、角、点的坐标等。要特别注意消参前后保持范围的等价性。多参问题中,根据方程的观点,引入n个参数,需建立n+1个方程,才能消参(特殊情况下,能整体处理时,方程个数可减少)。
5、交轨法:
求两动曲线交点轨迹时,可由方程直接消去参数,例如求两动直线的交点时常用此法,也可以引入参数来建立这些动曲线的联系,然而消去参数得到轨迹方程。可以说是参数法的一种变种。用交轨法求交点的轨迹方程时,不一定非要求出交点坐标,只要能消去参数,得到交点的两个坐标间的关系即可。交轨法实际上是参数法中的一种特殊情况。
求轨迹方程的步骤:
(l)建系,设点建立适当的坐标系,设曲线上任意一点的坐标为M(x,y);
(2)写集合写出符合条件P的点M的集合{M|P(M)};
(3)列式用坐标表示P(M),列出方程f(x,y)=0;
(4)化简化方程f(x,y)=0为最简形式;
(5)证明证明以化简后的方程的解为坐标的点都是曲线上的点,
与“若x、y∈R,且2y是1+x和1-x的等比中项,则动点(x,y)的轨迹...”考查相似的试题有:
- 设数列是等比数列,则“”是数列是递增数列的A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件
- 若数列是公比为4的等比数列,且,则数列是( )A.公差为2的等差数列B.公差为的等差数列C.公比为2的等比数列D.公比为的等...
- 已知数列{an}前n项和Sn满足an=2-2Sn.(I)求a1,a2;(II)求通项公式an;(III)求证数列{Sn-1}为等比数列.
- 在等比数列中—,则=A.8B.16C.D.
- 已知等比数列满足,且是,的等差中项.(Ⅰ)求数列的通项公式;(Ⅱ)若,,求使成立的的最小值.
- (本题满分14分)数列满足.(1)求数列{}的通项公式;(2)设数列{}的前项和为,证明.
- 已知数列。(1)求的值;(2)猜想的表达式并用数学归纳法证明。
- (本小题满分10分)数列中a1="8," a4="2," 且满足(n∈N*),(1)求数列通项公式;(2)设, 求.
- 已知数列满足,.(1)求的值,由此猜测的通项公式,并证明你的结论;(2)证明:.
- 在等比数列中,若,,则 ▲ .