本试题 “等比数列{an}中,“a1<a3”是“a5<a7”的( )A.充分而不必要条件B.必要而不充分条件C.充要条件D.既不充分也不必要条件” 主要考查您对充分条件与必要条件
等比数列的定义及性质
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 充分条件与必要条件
- 等比数列的定义及性质
1、充分条件与必要条件:一般地,“若p,则q”为真命题,是指由p通过推理可以得出q,这时,我们就说,由p可推出q,记作 ,并且说p是q的充分条件,q是p的必要条件;
,并且说p是q的充分条件,q是p的必要条件;
2、充要条件:一般地,如果既有 ,又有
,又有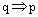 ,就记作
,就记作 ,此时,我们说,p是q的充分必要条件,简称充要条件。
,此时,我们说,p是q的充分必要条件,简称充要条件。
概括的说,如果 ,那么p与q互为充要条件。
,那么p与q互为充要条件。
3、充分不必要条件、必要不充分条件、既不充分也不必要条件:
①充分不必要条件:如果 ,且p
,且p q,则说p是q的充分不必要条件;
q,则说p是q的充分不必要条件;
②必要不充分条件:如果p q,且
q,且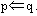 ,则说p是q的必要不充分条件;
,则说p是q的必要不充分条件;
③既不充分也不必要条件:如果p q,且p
q,且p q,则说p是q的既不充分也不必要条件。
q,则说p是q的既不充分也不必要条件。
等比数列的定义:
一般地,如果一个数列从第2项起,每一项与它的前一项的比等于同一个常数,那么这个数列就叫做等比数列,这个常数叫做公比,公比通常用字母q表示(q≠0)。
等比数列的性质:
在等比数列{an}中,有
(1)若m+n=p+q,m,n,p,q∈N*,则aman=apaq;当m+n=2p时,aman=ap2;
(2)若m,n∈N*,则am=anqm-n;
(3)若公比为q,则{ }是以
}是以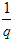 为公比的等比数列;
为公比的等比数列;
(4)下标成等差数列的项构成等比数列;
(5)
1)若a1>0,q>1,则{an}为递增数列;
2)a1<0,q>1, 则{an}为递减数列;
3)a1>0,0<q<1,则{an}为递减数列;
4)a1<0, 0<q<1, 则{an}为递增数列;
5)q<0,则{an}为摆动数列;若q=1,则{an}为常数列。
等差数列和等比数列的比较:
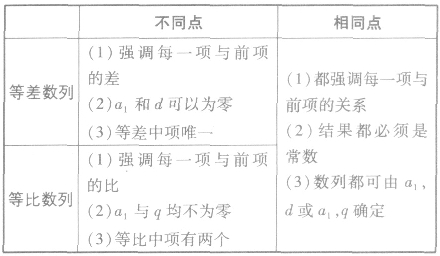
如何证明一个数列是等比数列:
证明一个数列是等比数列,只需证明 是一个与n无关的常数即可(或an2=an-1an+1)。
是一个与n无关的常数即可(或an2=an-1an+1)。
发现相似题
与“等比数列{an}中,“a1<a3”是“a5<a7”的( )A.充分而不必要...”考查相似的试题有:
- 设a,b是两个单位向量,命题“(2a+b)⊥b”是命题“a,b的夹角等于”成立的[ ]A.充分不必要条件B.必要不充分条件C.充要条件D.既不...
- 已知f(x)=sin(x+φ)(φ∈R),则“φ=π2”是“f(x)是偶函数”的( )A.充分不必要条件B.必要不充分条件C.充分必要条件D.既...
- 实数,条件:,条件:,则是的( )A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件
- 已知数列和满足:, 其中为实数,为正整数.(Ⅰ)对任意实数,证明数列不是等比数列;(Ⅱ)对于给定的实数,试求数列的前项和...
- 数列{an}满足a1=2,a2=5,an+2=3an+1-2an,(1)求证:数列{an+1-an}是等比数列;(2)求数列{an}的通项公式.
- (本小题满分14分)在数列中,=0,且对任意k,成等差数列,其公差为2k.(Ⅰ)证明成等比数列;(Ⅱ)求数列的通项公式;(Ⅲ)记...
- (本小题15分)已知,是实数,方程有两个实根,,数列满足,,(Ⅰ)求数列的通项公式(用,表示);(Ⅱ)若,,求的前项和.
- (本小题满分14分)已知数列满足,.(1)求数列的通项公式;(2)设,求数列的前项和.
- (本小题满分14分)已知数列的前项和为,且. (1)求数列的通项公式;(2)设数列满足:,求证:;(3)求证:]
- 在等比数列中,,则( ).A.B.C.D.