本试题 “已知函数f(x)=bx-5x+a(x≠-a,a、b是常数,且ab≠-5),对定义域内任意x(x≠-a、x≠-a-3且x≠a+3),恒有f(3+x)+f(3-x)=4成立.(1)求函数y=f(x)的解析式...” 主要考查您对集合间的基本关系
函数的定义域、值域
函数解析式的求解及其常用方法
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 集合间的基本关系
- 函数的定义域、值域
- 函数解析式的求解及其常用方法
集合与集合的关系有“包含”与“不包含”,“相等”三种:
1、 子集概念:
一般地,对于两个集合A与B,如果集合A的任何一个元素都是集合B的元素,就说集合B包含A,记作A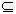 B(或说A包含于B),
B(或说A包含于B),
也可记为B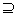 A(B包含A),此时说A是B的子集;A不是B的子集,记作A
A(B包含A),此时说A是B的子集;A不是B的子集,记作A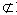 B,读作A不包含于B
B,读作A不包含于B
2、集合相等:
对于集合A和B,如果集合A中的每一个元素都是集合B的元素,反过来,集合B的每一个元素也都是集合A的元素,即集合A是集合B的子集,且集合B是集合A的子集,我么就说集合A和集合B相等,记作A=B
3、真子集:
对于集合A与B,如果A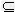 B并且A≠B,则集合A是集合B的真子集,记作A
B并且A≠B,则集合A是集合B的真子集,记作A B(B
B(B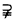 A),读作A真包含于B(B真包含A)
A),读作A真包含于B(B真包含A)
集合间基本关系:
性质1:
(1)空集是任何集合的子集,即A;
(2)空集是任何非空集合的真子集;
(3)传递性:AB,BCAC;AB,BCAC;
(4)AB,BAA=B。
性质2:
子集个数的运算:含n个元素的集合A的子集有2n个,非空子集有2n-1个,非空真子集有2n-2个。
集合间基本关系性质:
(1)空集是任何集合的子集,即A;
(2)空集是任何非空集合的真子集;
(3)传递性: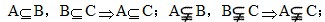
(4)集合相等:
(5)含n个元素的集合A的子集有2n个,非空子集有2n-1个,非空真子集有2n-2个。
定义域、值域的概念:
自变量取值范围叫做函数的定义域,函数值的集合叫做函数的值域。
1、求函数定义域的常用方法有:
(1)根据解析式要求如偶次根式的被开方大于零,分母不能为零等;
(2)根据实际问题的要求确定自变量的范围;
(3)根据相关解析式的定义域来确定所求函数自变量的范围;
(4)复合函数的定义域:如果y是u的函数,而u是x的函数,即y=f(u),u=g(x),那么y=f[g(x)]叫做函数f与g的复合函数,u叫做中间变量,设f(x)的定义域是x∈M,g(x)的定义域是x∈N,求y=f[g(x)]的定义域时,则只需求满足 的x的集合。设y=f[g(x)]的定义域为P,则
的x的集合。设y=f[g(x)]的定义域为P,则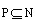 。
。
3、求函数值域的方法:
(1)利用一些常见函数的单调性和值域,如一次函数,二次函数,反比例函数,指数函数,对数函数,三角函数,形如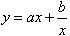 (a,b为非零常数)的函数;
(a,b为非零常数)的函数;
(2)利用函数的图象即数形结合的方法;
(3)利用均值不等式;
(4)利用判别式;
(5)利用换元法(如三角换元);
(6)分离法:分离常数与分离参数两种形式;
(7)利用复合函数的单调性。(注:二次函数在闭区间上的值域要特别注意对称轴与闭区间的位置关系,含字母时要注意讨论)
函数解析式的常用求解方法:
(1)待定系数法:(已知函数类型如:一次、二次函数、反比例函数等):若已知f(x)的结构时,可设出含参数的表达式,再根据已知条件,列方程或方程组,从而求出待定的参数,求得f(x)的表达式。待定系数法是一种重要的数学方法,它只适用于已知所求函数的类型求其解析式。
(2)换元法(注意新元的取值范围):已知f(g(x))的表达式,欲求f(x),我们常设t=g(x),从而求得 ,然后代入f(g(x))的表达式,从而得到f(t)的表达式,即为f(x)的表达式。
,然后代入f(g(x))的表达式,从而得到f(t)的表达式,即为f(x)的表达式。
(3)配凑法(整体代换法):若已知f(g(x))的表达式,欲求f(x)的表达式,用换元法有困难时,(如g(x)不存在反函数)可把g(x)看成一个整体,把右边变为由g(x)组成的式子,再换元求出f(x)的式子。
(4)消元法(如自变量互为倒数、已知f(x)为奇函数且g(x)为偶函数等):若已知以函数为元的方程形式,若能设法构造另一个方程,组成方程组,再解这个方程组,求出函数元,称这个方法为消元法。
(5)赋值法(特殊值代入法):在求某些函数的表达式或求某些函数值时,有时把已知条件中的某些变量赋值,使问题简单明了,从而易于求出函数的表达式。
与“已知函数f(x)=bx-5x+a(x≠-a,a、b是常数,且ab≠-5),对定义...”考查相似的试题有:
- 设集合A={x||x-a|<1,x∈R} ,B={x||x-b|>2,x∈R},若AB,则实数a,b必满足[ ]A.|a+b|≤3B.|a+b|≥3C.|a-b|≤3D.|a-b|≥3
- 设解不等式:
- (1)求函数的表达式,并求其定义域。(2)当时,求函数的值域
- 已知函数f(x)=2x-1的反函数为f-1(x),g(x)=log4(3x+1).(1)若f-1(x)≤g(x),求x的取值范围P;(2)设h(x)=g(x)-...
- 已知函数f(x)=1+1x-1,g(x)=f(2|x|).(I)求函数f(x)和g(x)的定义域;(II)函数f(x)和g(x)是否具有奇偶性,并说明...
- 已知函数f(x+1)=x+3x+4,试求函数y=f(x)的解析式及其最小值.
- 函数的定义域是 .
- 已知函数f(x)=2x3+ax与g(x)=bx2+c的图象都经过点P(2,0),且在点P处有公切线,求f(x),g(x)的表达式及点P处的公切...
- 已知f(x)是一次函数,且f(0)=3,f(1)=5.(1)求f(x)的解析式;(2)画出此函数的图象,根据图象直接说出此函数在R上...
- 已知函数f(x)=2f′(1)ex-1-x,e≈2.7.(1)已知函数f(x)的解析式及单调区间;(2)若对任意的x∈[12,+∞),e2f(x)≥(a-e2)...