等比数列的通项公式:

a_n=a₁q^n-1，q≠0，n∈N^*。

等比数列的通项公式的理解：

①在已知a₁和q的前提下，利用通项公式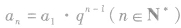可求出等比数列中的任意一项；
②在已知等比数列中任意两项的前提下，使用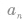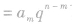可求等比数列中任何一项；
③用函数的观点看等比数列的通项，等比数列{a_n}的通项公式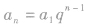，可以改写为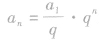．当q>o，且q≠1时，y=q^x是一个指数函数，而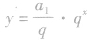是一个不为0的常数与指数函数的积，因此等比数列{a_n}的图象是函数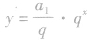的图象上的一群孤立的点；
④通项公式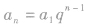亦可用以下方法推导出来：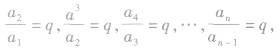

将以上（n一1）个等式相乘，便可得到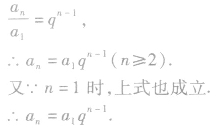
 
⑤用方程的观点看通项公式．在a_n，q，a₁，n中，知三求一。

等比数列的前n项和公式：

；

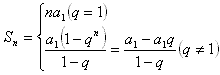等比数列中设元技巧：

已知a₁，q，n，a_n ，S_n中的三个量，求其它两个量，是归结为解方程组问题，知三求二。
注意设元的技巧，如奇数个成等比数列，可设为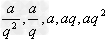：…，…（公比为q），但偶数个数成等比数列时，不能设为…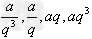，…因公比不一定为一个正数，公比为正时可如此设。

等比数列前n项和公式的变形：
q≠1时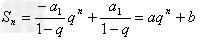，（a≠0，b≠0，a+b=0）；

等比数列前n项和常见结论：
一个等比数列有3n项，若前n项之和为S₁，中间n项之和为S₂，最后n项之和为S₃，当q≠-1时，S₁，S₂，S₃为等比数列。