本试题 “如图,椭圆的中心为原点O,离心率e=,一条准线的方程是x=,(Ⅰ)求椭圆的标准方程;(Ⅱ)设动点P满足:,其中M,N是椭圆上的点,直线OM与ON的斜率之积为。问:是...” 主要考查您对向量的线性运算及坐标表示
椭圆的定义
椭圆的标准方程及图象
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 向量的线性运算及坐标表示
- 椭圆的定义
- 椭圆的标准方程及图象
向量的线性运算:
向量的线性运算是指向量的加、减、数乘的运算;对于任意向量a,b以及任意实数

向量的线性运算的坐标表示:
设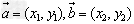 ,任意实数λ,m,n,则
,任意实数λ,m,n,则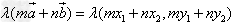 。
。
平面向量的几个重要结论:
(1)若a、b为不共线向量,则a+b、a-b是以a、b为邻边的平行四边形的对角线的向量.如图: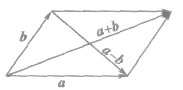
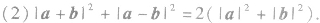

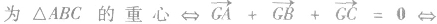
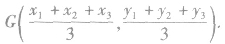
椭圆的第一定义:
平面内与两个定点为F1,F2的距离的和等于常数(大于 )的轨迹叫做椭圆,这两个定点叫做椭圆的焦点,两焦点的距离叫做椭圆的焦距。特别地,当常数等于
)的轨迹叫做椭圆,这两个定点叫做椭圆的焦点,两焦点的距离叫做椭圆的焦距。特别地,当常数等于 时,轨迹是线段F1F2,当常数小于
时,轨迹是线段F1F2,当常数小于 时,无轨迹。
时,无轨迹。
椭圆的第二定义:
平面内到定点F的距离和到定直线l的距离之比等于常数e(0<e<1)的点的轨迹,叫做椭圆,定点F叫椭圆的焦点,定直线l叫做椭圆的准线,e叫椭圆的离心率。
椭圆的定义应该包含几个要素:
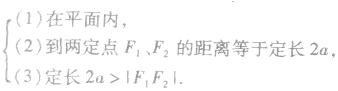
利用椭圆的定义解题:
当题目中出现一点在椭圆上的条件时,注意使用定义

椭圆的标准方程:
(1)中心在原点,焦点在x轴上: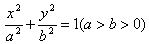 ;
;
(2)中心在原点,焦点在y轴上: 。
。
椭圆的图像:
(1)焦点在x轴: ;
;
(2)焦点在y轴: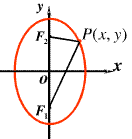 。
。
巧记椭圆标准方程的形式:
①椭圆标准方程的形式:左边是两个分式的平方和,右边是1;
②椭圆的标准方程中,x2与y2的分母哪一个大,则焦点在哪一个轴上;
③椭圆的标准方程中,三个参数a,b,c满足a2= b2+ c2;
④由椭圆的标准方程可以求出三个参数a,b,c的值.
待定系数法求椭圆的标准方程:
求椭圆的标准方程常用待定系数法,要恰当地选择方程的形式,如果不能确定焦点的位置,那么有两种方法来解决问题:一是分类讨论,全面考虑问题;二是可把椭圆的方程设为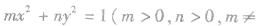 n)用待定系数法求出m,n的值,从而求出标准方程,
n)用待定系数法求出m,n的值,从而求出标准方程,
发现相似题
与“如图,椭圆的中心为原点O,离心率e=,一条准线的方程是x=,(Ⅰ...”考查相似的试题有:
- P(x0,y0)(x0≠±a)是双曲线E:上一点,M,N分别是双曲线E的左、右定点,直线PM,PN的斜率之积为,(1)求双曲线的离心率;...
- 已知是椭圆()的半焦距,则的取值范围是___________
- 已知椭圆的短半轴长为,离心率满足,求长轴的最大值。
- 已知椭圆的离心率为,且过点.(1)求椭圆的方程;(2)若过点C(-1,0)且斜率为的直线与椭圆相交于不同的两点,试问在轴上是...
- 、设椭圆,双曲线,抛物线(其中的离心率分别为,则的值为 ( ) 与有关
- 如图,设P是圆上的动点,点D是P在轴上投影,M为PD上一点,且.(1)当P在圆上运动时,求点M的轨迹C的方程;(2)求过点(...
- 直线l:2x-3y+12=0与x轴、y轴分别交于A、B两点,则以A为焦点,经过B点的椭圆的标准方程是______.
- 已知在平面直角坐标系中的一个椭圆,它的中心在原点,左焦点为F(-3,0),且过D(2,0),设点A(1,12).(1)求该椭圆的...
- 已知双曲线x26-y22=1,(1)求以双曲线的顶点为焦点,焦点为顶点的椭圆E的方程.(2)点P在椭圆E上,点C(2,1)关于坐标原点...
- 已知动圆M经过点G(0,-1),且与圆Q:x2+(y-1)2=8内切.(Ⅰ)求动圆M的圆心的轨迹E的方程.(Ⅱ)以m=(1,2)为方向向量的直...