本试题 “已知|a|=2,|b|=1,a与b的夹角为60°,则使向量a+λb与λa-2b的夹角为钝角的λ范围是( )A.(-∞,-1-3)B.(-1+3,+∞)C.(-∞,-1-3)∪(-1+3,+∞)D.(-1-3...” 主要考查您对用数量积表示两个向量的夹角
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 用数量积表示两个向量的夹角
用数量积表示两个向量的夹角:
设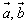 都是非零向量,
都是非零向量,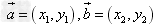 ,θ是
,θ是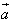 与
与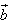 的夹角,根据向量数量积的定义及坐标表示可得
的夹角,根据向量数量积的定义及坐标表示可得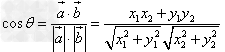 。
。
向量数量积问题中方法提炼:
(1)平面向量的数量积的运算有两种形式,一是依据定义来计算,二是利用坐标来计算,具体应用哪种形式应根据已知条件的特征来选择;
(2)平面向量数量积的计算类似于多项式的运算,解题中要注意多项式运算方法的运用;
(3)平面向量数量积的计算中要注意平面向量基本定理的应用,选择合适的基底,以简化运算
(4)向量的数量积是一个数而不是一个向量。
发现相似题
与“已知|a|=2,|b|=1,a与b的夹角为60°,则使向量a+λb与λa-2b的...”考查相似的试题有:
- 若向量=(1,1),=(4,2),则向量,的夹角的余弦值为( )。
- 已知向量a,b满足|a|=1,|a+b|=7,且a,b的夹角为π3,则|b|=______.
- 已知|a|=1,|b|=2,(1)若a∥b,求a•b;(2)若a,b的夹角为135°,求|a+b|.
- 设i、j是平面直角坐标系(坐标原点为O)内分别与x轴、y轴正方向相同的两个单位向量,且OA=-2i+j,OB=4i+3j,则△OAB的面积等于...
- 已知a,b均为非零向量,满足|a|=|b|=|a+b|,求a与a-b的夹角.
- 设A,B,C,D是空间不共面的四点,且满足,则△BCD是( ) A.钝角三角形 B.直角三角形 C.锐角三角形 D.不确定
- 若a 、 b是单位向量,且a•b=-12,则向量a 、 b的夹角α=______.
- 已知a=(1,-2),b=(x,y),(Ⅰ)若x是从-1,0,1,2四个数中任取的一个数,y是从-1,0,1三个数中任取的一个数,求a⊥b的概率...
- 已知向量a=(12x,x-4),向量b=(x,32x),x∈[-4,5](Ⅰ)试用x表示a•b;(Ⅱ)求a•b的最大值,并求此时的cos<a、b>.(<...
- 已知△ABC的三个内角分别为A,B,C,向量m=(sinB,1-cosB)与向量n=(2,0)夹角的余弦角为12.(1)求角B的大小;(2)求sinA+si...