本试题 “已知|a|=1,|b|=2,(1)若a∥b,求a•b;(2)若a,b的夹角为135°,求|a+b|.” 主要考查您对用数量积表示两个向量的夹角
向量数量积的运算
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 用数量积表示两个向量的夹角
- 向量数量积的运算
用数量积表示两个向量的夹角:
设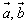 都是非零向量,
都是非零向量,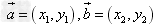 ,θ是
,θ是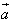 与
与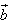 的夹角,根据向量数量积的定义及坐标表示可得
的夹角,根据向量数量积的定义及坐标表示可得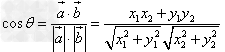 。
。
向量数量积问题中方法提炼:
(1)平面向量的数量积的运算有两种形式,一是依据定义来计算,二是利用坐标来计算,具体应用哪种形式应根据已知条件的特征来选择;
(2)平面向量数量积的计算类似于多项式的运算,解题中要注意多项式运算方法的运用;
(3)平面向量数量积的计算中要注意平面向量基本定理的应用,选择合适的基底,以简化运算
(4)向量的数量积是一个数而不是一个向量。
两个向量数量积的含义:
如果两个非零向量 ,
, ,它们的夹角为
,它们的夹角为 ,我们把数量
,我们把数量 叫做
叫做 与
与 的数量积(或内积或点积),记作:
的数量积(或内积或点积),记作: ,即
,即 。
。 叫
叫 在
在 上的投影。
上的投影。
规定:零向量与任一向量的数量积是0,注意数量积是一个实数,不再是一个向量。
数量积的的运算律:
已知向量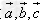 和实数λ,下面(1)(2)(3)分别叫做交换律,数乘结合律,分配律。
和实数λ,下面(1)(2)(3)分别叫做交换律,数乘结合律,分配律。
(1)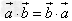 ;
;
(2)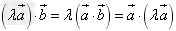 ;
;
(3)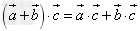 。
。
向量数量积的性质:
设两个非零向量
(1) ;
;
(2) ;
;
(3) ;
;
(4) ;
;
(5)当 ,
, 同向时,
同向时, ;当
;当 与
与 反向时,
反向时, ;当
;当 为锐角时,
为锐角时, 为正且
为正且 ,
, 不同向,
不同向, ;当
;当 为钝角时,
为钝角时, 为负且
为负且 ,
, 不反向,
不反向, 。
。
发现相似题
与“已知|a|=1,|b|=2,(1)若a∥b,求a•b;(2)若a,b的夹角为1...”考查相似的试题有:
- 平面向量a=(3,-4),b=(2,x),c=(2,y),已知a∥b,a⊥c,求b和c的坐标及b与c夹角.
- 连掷两次骰子分别得到点数m、n,向量a=(m,n),b=(-1,1)若△ABC中AB 与a同向,CB 与b反向,则∠ABC是钝角的概率是( )A....
- 已知平面上三点A、B、C满足|AB|=2,|BC|=1,|CA|=3,则AB•BC+BC•CA+CA•AB的值等于______.
- 已知△ABC的周长为6,|BC| ,|CA| ,|AB|成等比数列,求(I)试求∠B的取值范围;(Ⅱ)求BA•BC的取值范围.
- 在三角形ABC中,AB、BC、CA的长分别为c、a、b且b=4,c=5,∠A=45°,则AB•CA=______.
- 已知向量a=(12x,x-4),向量b=(x,32x),x∈[-4,5](Ⅰ)试用x表示a•b;(Ⅱ)求a•b的最大值,并求此时的cos<a、b>.(<...
- 已知、分别为x轴、y轴方向上的单位向量,若+=2-8,-=-8+16,那么·等于( ) A.63 B.-63 C.33 D.-33
- 若向量a=(1,1),b(-1,2),则a•b等于______.
- 已知|AC|=5,|AB|=8,AD=511DB,CD•AD=0,(1)求|AB-AC|;(2)设∠BAC=θ,且已知cos(θ+x)=45,-π<x<-π4,求sinx.
- 已知F1,F2是椭圆x2a2+y2b2=1(a>b>0)的两个焦点,O为坐标原点,点P(-1,22)在椭圆上,且PF1•F1F2=0,⊙O是以F1F2为直径...