返回

高中三年级数学

首页
首页 高中三年级数学知识 等差数列的通项公式 等比数列的通项公式 综合法与分析法证明不等式 试题正文
  • 解答题
    已知数列{}的前n项和为=（n∈N*），且a1=2．数列{bn}满足b1=0，b2=2，=，n=2，3，…．
    （Ⅰ）求数列 {} 的通项公式；
    （Ⅱ）求数列 {bn} 的通项公式；
    （Ⅲ）证明：对于 n∈N*，．
    本题信息：2011年江西省同步题数学解答题难度极难 来源:吴凯忠（高中数学）
  • 本题答案
    查看答案
本试题 “已知数列{}的前n项和为=（n∈N*），且a1=2．数列{bn}满足b1=0，b2=2，=，n=2，3，…．（Ⅰ）求数列 {} 的通项公式；（Ⅱ）求数列 {bn} 的通项公式；（Ⅲ）证明：对...” 主要考查您对

等差数列的通项公式

等比数列的通项公式

综合法与分析法证明不等式

等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
  • 等差数列的通项公式
  • 等比数列的通项公式
  • 综合法与分析法证明不等式

等差数列的通项公式:

an=a1+（n-1）d，n∈N*。
an=dn+a1-d，d≠0时，是关于n的一次函数，斜率为公差d；
an=kn+b（k≠）｛an｝为等差数列，反之不能。


对等差数列的通项公式的理解：

 ①从方程的观点来看，等差数列的通项公式中含有四个量，只要已知其中三个，即可求出另外一个．其中a1和d是基本量，只要知道a1和d即可求出等差数列的任一项；
②从函数的观点来看，在等差数列的通项公式中，。。是n的一次函数，其图象是直线y=dx+（a1-d）上均匀排开的一列孤立点，我们知道两点确定一条直线，因此，给出一个等差数列的任意两项，等差数列就被唯一确定了，


等差数列公式的推导：

等差数列的通项公式可由归纳得出，当然，等差数列的通项公式也可用累加法得到：


等比数列的通项公式:

an=a1qn-1，q≠0，n∈N*。


等比数列的通项公式的理解：

①在已知a1和q的前提下，利用通项公式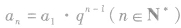可求出等比数列中的任意一项；
②在已知等比数列中任意两项的前提下，使用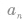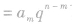可求等比数列中任何一项；
③用函数的观点看等比数列的通项，等比数列{an}的通项公式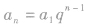，可以改写为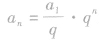．当q>o，且q≠1时，y=qx是一个指数函数，而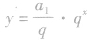是一个不为0的常数与指数函数的积，因此等比数列{an}的图象是函数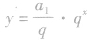的图象上的一群孤立的点；
④通项公式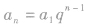亦可用以下方法推导出来：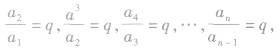

将以上（n一1）个等式相乘，便可得到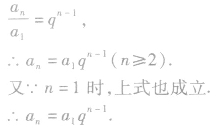
 
⑤用方程的观点看通项公式．在an，q，a1，n中，知三求一。


综合法：

利用某些已知的不等式或已证过的不等式或不等式的性质推导出所要证的不等式成立，这种证明方法叫综合法，即由因导果。利用均值不等式的有关公式最为常见。

分析法：

（1）从求证的不等式出发，分析使这个不等式成立的充分条件，把证明这个不等式的问题转化为这些条件是否具备的问题，如果能肯定这些条件都已具备，那么就可以判定所证的不等式成立，这种证明方法叫分析法，即执果索因；
（2）用分析法证明要注意格式：“若A成立，则B成立”的模式是：欲证B为真，只需证C为真，只需证D为真…最后得出A或已知的性质、公理、定理，从而得出B为真。也可使用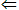简化叙述。即BCD…A或已知的性质、公理、定理。切不可使用BCD…A。


用综合法分析法证明不等式常用到的结论：

 
 
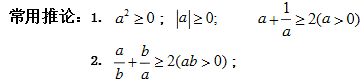
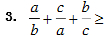                      3，

发现相似题
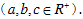
与“已知数列{}的前n项和为=（n∈N*），且a1=2．数列{bn}满足b1=0...”考查相似的试题有：