返回

高中二年级数学

首页
首页 高中二年级数学知识 基本不等式及其应用 直线的方程 两点间的距离 试题正文
  • 解答题
    直线l过点P（2，1），且分别与x，y轴的正半轴于A，B两点，O为原点．
    （1）求△AOB面积最小值时l的方程；
    （2）|PA||PB|取最小值时l的方程．
    本题信息：2012年江苏期中题数学解答题难度较难 来源:沈诺（高中数学）
  • 本题答案
    查看答案
本试题 “直线l过点P（2，1），且分别与x，y轴的正半轴于A，B两点，O为原点．（1）求△AOB面积最小值时l的方程；（2）|PA||PB|取最小值时l的方程．” 主要考查您对

基本不等式及其应用

直线的方程

两点间的距离

等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
  • 基本不等式及其应用
  • 直线的方程
  • 两点间的距离

基本不等式：

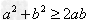（当且仅当a＝b时取“=”号）；
变式：①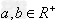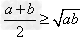，（当且仅当a＝b时取“=”号），即两个正数的算术平均不小于它们的几何平均。
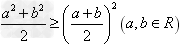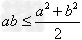②；③；④；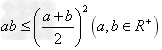


对基本不等式的理解：

(1)基本不等式的证明是利用重要不等式推导的，即，即有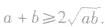
(2)基本不等式又称为均值定理、均值不等式等，其中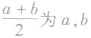的算术平均数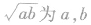，的几何平均数，本定理也可叙述为：两个正数的算术平均数不小于它们的几何平均数．
(3)要特别注意不等式成立的条件和等号成立的条件．均值不等式中：①当a=b时取等号，即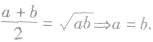


对于两个正数x，y，若已知xy，x+y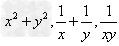，中的某一个为定值，可求出其余各个的最值：
如：（1）当xy＝P（定值），那么当x=y时，和x+y有最小值2，；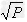
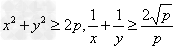（2）x+y=S（定值），那么当x=y时，积xy有最大值，；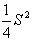
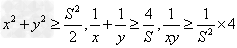（3）已知x2+y2=p，则x+y有最大值为，。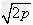

应用基本的不等式解题时：

注意创设一个应用基本不等式的情境及使等号成立的条件，即“一正、二定、三相等”。

利用基本不等式比较实数大小：

(1)注意均值不等式的前提条件．
(2)通过加减项的方法配凑成使用均值定理的形式．
(3)注意“1”的代换．
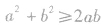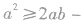
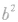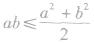(4)灵活变换基本不等式的形式，并注重其变形形式的运用．重要不等式的形式可以是，也可以是，还可以是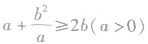等，不仅要掌握原来的形式，还要掌握它的几种变形形式以及公式的逆用等，以便应用．
(5)合理配组，反复应用均值不等式。 


基本不等式的几种变形公式：
 
 

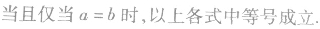
直线方程的定义：

以一个方程的解为坐标的点都是某条直线上的点，这个方程就叫做这条直线的方程，这条直线叫做这个方程的直线。

基本的思想和方法：

求直线方程是解析几何常见的问题之一，恰当选择方程的形式是每一步，然后釆用待定系数法确定方程，在求直线方程时，要注意斜率是否存在，利用截距式时，不能忽视截距为0的情形，同时要区分“截距”和“距离”。

直线方程的几种形式：

1.点斜式方程：
（1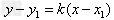），（直线l过点，且斜率为k）。
（2）当直线的斜率为0°时，k=0，直线的方程是y=y1。当直线的斜率为90°时，直线的斜率不存在，它的方程不能用点斜式表示，但因l上每一点的横坐标都等于x1，所以它的方程是x=x1。
2.斜截式方程：已知直线在y轴上的截距为b和斜率k，则直线的方程为：y=kx+b，它不包括垂直于x轴的直线。
3.两点式方程：已知直线经过（x1，y1），（x2，y2）两点，则直线方程为：
4.截距式方程：已知直线在x轴和y轴上的截距为a，b，则直线方程为：（a、b≠0）。
5.一般式方程：（1）定义：任何直线均可写成：Ax+By+C=0（A，B不同时为0）的形式。（2）特殊的方程如：平行于x轴的直线：y=b（b为常数）；平行于y轴的直线：x=a（a为常数）。


几种特殊位置的直线方程：

 
求直线方程的一般方法:
 
(1)直接法：根据已知条件，选择适当的直线方程形式，直接求出直线方程．应明确直线方程的几种形式及各自的特点，合理选择解决方法，一般地，已知一点通常选择点斜式；已知斜率选择斜截式或点斜式；已知在两坐标轴上的截距用截距式；已知两点用两点式，这时应特别注意斜率不存在的情况．
(2)待定系数法：先设出直线的方程，再根据已知条件求出假设系数，最后代入直线方程，待定系数法常适用于斜截式，已知两点坐标等．
利用待定系数法求直线方程的步骤：①设方程；②求系数；③代入方程得直线方程，如果已知直线过一个定点,可以利用直线的点斜式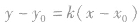求方程，也可以利用斜截式、截距式等形式求解．

两点间的距离公式：

设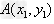，是平面直角坐标系中的两个点，则。
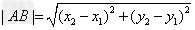特别地，原点O（0,0）与任意一点P（x,y）的距离为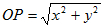


两点间的距离公式的理解：

（1）在公式中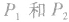，的位置是对称的，没有先后之分，即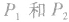间的距离也可表示为
（2）


发现相似题
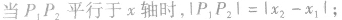
与“直线l过点P（2，1），且分别与x，y轴的正半轴于A，B两点，O为...”考查相似的试题有：