返回

高中数学

首页
首页 高中数学知识 等差数列的定义及性质 等差数列的通项公式 数列的概念及简单表示法 试题正文
  • 解答题
    已知数列{an}中，a1=
    3
    5
    ，an=2-
    1
    an-1
    (n≥2，n∈N+)    ，数列{bn}满足：bn=
    1
    an-1
    (n∈N+)    ；
    （1）求证：数列{bn}是等差数列；
    （2）求数列{an}的通项an；
    （3）求数列{an}中的最大项和最小项，并说明理由．
    本题信息：数学解答题难度较难 来源:未知
  • 本题答案
    查看答案
本试题 “已知数列{an}中，a1=35，an=2-1an-1(n≥2，n∈N+)，数列{bn}满足：bn=1an-1(n∈N+)；（1）求证：数列{bn}是等差数列；（2）求数列{an}的通项an；（3）求数列{an}...” 主要考查您对

等差数列的定义及性质

等差数列的通项公式

数列的概念及简单表示法

等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
  • 等差数列的定义及性质
  • 等差数列的通项公式
  • 数列的概念及简单表示法

等差数列的定义：

一般地，如果一个数列从第2项起，每一项与它的前一项的差等于同一个常数，那么这个数列就叫做等差数列，这个常数叫做公差，用符号语言表示为an+1-an=d。


等差数列的性质：

（1）若公差d＞0，则为递增等差数列；若公差d＜0，则为递减等差数列；若公差d＝0，则为常数列；
（2）有穷等差数列中，与首末两端“等距离”的两项和相等，并且等于首末两项之和；
（3）m，n∈N*，则am＝an+(m-n)d；
（4）若s，t，p，q∈N*，且s+t=p+q，则as+at=ap+aq，其中as，at，ap，aq是数列中的项，特别地，当s+t=2p时，有as+at=2ap；
（5）若数列｛an｝，｛bn｝均是等差数列，则数列｛man+kbn｝仍为等差数列，其中m，k均为常数。
（6）
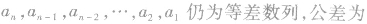
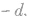
（7）从第二项开始起，每一项是与它相邻两项的等差中项，也是与它等距离的前后两项的等差中项，即
（8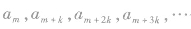） 仍为等差数列，公差为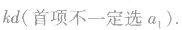


 


对等差数列定义的理解：

①如果一个数列不是从第2项起，而是从第3项或某一项起，每一项与它前一项的差是同一个常数，那么此数列不是等差数列，但可以说从第2项或某项开始是等差数列． 
②求公差d时，因为d是这个数列的后一项与前一项的差，故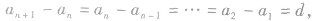有 还有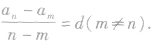
③公差d∈R，当d=0时，数列为常数列（也是等差数列）；当d>0时，数列为递增数列；当d<0时，数列为递减数列；
④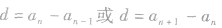 是证明或判断一个数列是否为等差数列的依据；
⑤证明一个数列是等差数列，只需证明an+1-an是一个与n无关的常数即可。

等差数列求解与证明的基本方法：

(1)学会运用函数与方程思想解题；
(2)抓住首项与公差是解决等差数列问题的关键；
(3)等差数列的通项公式、前n项和公式涉及五个量：a1，d，n，an，Sn，知道其中任意三个就可以列方程组求出另外两个(俗称“知三求二’)．


等差数列的通项公式:

an=a1+（n-1）d，n∈N*。
an=dn+a1-d，d≠0时，是关于n的一次函数，斜率为公差d；
an=kn+b（k≠）｛an｝为等差数列，反之不能。


对等差数列的通项公式的理解：

 ①从方程的观点来看，等差数列的通项公式中含有四个量，只要已知其中三个，即可求出另外一个．其中a1和d是基本量，只要知道a1和d即可求出等差数列的任一项；
②从函数的观点来看，在等差数列的通项公式中，。。是n的一次函数，其图象是直线y=dx+（a1-d）上均匀排开的一列孤立点，我们知道两点确定一条直线，因此，给出一个等差数列的任意两项，等差数列就被唯一确定了，


等差数列公式的推导：

等差数列的通项公式可由归纳得出，当然，等差数列的通项公式也可用累加法得到：


数列的定义：

一般地按一定次序排列的一列数叫作数列，数列中的每一个数叫作这个数列的项，数列的一般形式可以写成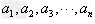，简记为数列{an}，其中数列的第一项a1也称首项，an是数列的第n项，也叫数列的通项2、数列的递推公式：如果已知数列的第1项（或前几项），且从第2项（或某一项）开始的任一项an与它的前一项an-1（或前几项）间的关系可以用一个公式表示，那么这个公式就叫做这个数列的递推公式，递推公式也是给出数列的一种方法。


从函数角度看数列：

数列可以看作是一个定义域为正整数集N'（或它的有限子集{l，2，3，…，n}）的函数，即当自变量从小到大依次取值时对应的一列函数值，这里说的函数是一种特殊函数，其特殊性为自变量只能取正整数，且只能从I开始依次增大．可以将序号作为横坐标，相应的项作为纵坐标描点画图来表示一个数列，从数列的图象可以看出数列中各项的变化情况。
特别提醒：
①数列是一个特殊的函数，因此在解决数列问题时，要善于利用函数的知识、函数的观点、函数的思想方法来解题，即用共性来解决特殊问题；
②还要注意数列的特殊性（离散型），由于它的定义域是N'或它的子集{1，2，…，n}，因而它的图象是一系列孤立的点，而不像我们前面所研究过的初等函数一般都是连续的曲线，因此在解决问题时，要充分利用这一特殊性．


发现相似题
与“已知数列{an}中，a1=35，an=2-1an-1(n≥2，n∈N+)，数列{bn}满...”考查相似的试题有：