本试题 “给出下列命题,其中正确的命题是 (写出正确命题的序号)①在△ABC中,若tanA+tanB+tanC0,则△ABC是锐角三角形;②在△ABC中,AB是cosAcosB的充要条件;③已知非零...” 主要考查您对充分条件与必要条件
正弦定理
用数量积表示两个向量的夹角
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 充分条件与必要条件
- 正弦定理
- 用数量积表示两个向量的夹角
1、充分条件与必要条件:一般地,“若p,则q”为真命题,是指由p通过推理可以得出q,这时,我们就说,由p可推出q,记作 ,并且说p是q的充分条件,q是p的必要条件;
,并且说p是q的充分条件,q是p的必要条件;
2、充要条件:一般地,如果既有 ,又有
,又有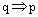 ,就记作
,就记作 ,此时,我们说,p是q的充分必要条件,简称充要条件。
,此时,我们说,p是q的充分必要条件,简称充要条件。
概括的说,如果 ,那么p与q互为充要条件。
,那么p与q互为充要条件。
3、充分不必要条件、必要不充分条件、既不充分也不必要条件:
①充分不必要条件:如果 ,且p
,且p q,则说p是q的充分不必要条件;
q,则说p是q的充分不必要条件;
②必要不充分条件:如果p q,且
q,且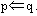 ,则说p是q的必要不充分条件;
,则说p是q的必要不充分条件;
③既不充分也不必要条件:如果p q,且p
q,且p q,则说p是q的既不充分也不必要条件。
q,则说p是q的既不充分也不必要条件。
正弦定理:
在一个三角形中,各边和它所对角的正弦的比相等,即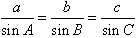 =2R。
=2R。
有以下一些变式:
(1)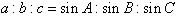 ;
;
(2)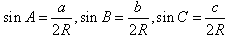 ;
;
(3)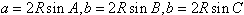 。
。
正弦定理在解三角形中的应用:
(1)已知两角和一边解三角形,只有一解。
(2)已知两边和其中一边的对角,解三角形,要注意对解的个数的讨论。可按如下步骤和方法进行:先看已知角的性质和已知两边的大小关系。
如已知a,b,A,
(一)若A为钝角或直角,当b≥a时,则无解;当a≥b时,有只有一个解;
(二)若A为锐角,结合下图理解。
①若a≥b或a=bsinA,则只有一个解。
②若bsinA<a<b,则有两解。
③若a<bsinA,则无解。 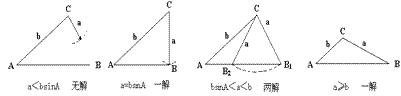
也可根据a,b的关系及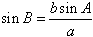 与1的大小关系来确定。
与1的大小关系来确定。
用数量积表示两个向量的夹角:
设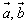 都是非零向量,
都是非零向量,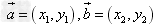 ,θ是
,θ是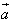 与
与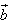 的夹角,根据向量数量积的定义及坐标表示可得
的夹角,根据向量数量积的定义及坐标表示可得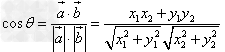 。
。
向量数量积问题中方法提炼:
(1)平面向量的数量积的运算有两种形式,一是依据定义来计算,二是利用坐标来计算,具体应用哪种形式应根据已知条件的特征来选择;
(2)平面向量数量积的计算类似于多项式的运算,解题中要注意多项式运算方法的运用;
(3)平面向量数量积的计算中要注意平面向量基本定理的应用,选择合适的基底,以简化运算
(4)向量的数量积是一个数而不是一个向量。
与“给出下列命题,其中正确的命题是 (写出正确命题的序号)①在△...”考查相似的试题有:
- “1<a<2”是“对任意的正数x,2”的A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件
- 设p:实数x满足x2+2ax-3a2<0(a>0),q:实数x满足1<5x+4,且¬p是¬q的必要不充分条件,求a的取值范围.
- “为锐角”是“”成立的 ( )A.充分不必要条件 B.必要不充分条件C.充要条件D.既不充分又不必要条件
- 已知直线丄平面,直线平面,则“”是“”的 ( )A.充要条件B.必要条件C.充分条件D.既不充分又不必要条件
- 已知α:x≥a,β:|x-1|<1.若α是β的必要非充分条件,则实数a的取值范围是______.
- 已知命题,命题,则下列说法正确的是( ▲ )A.是的充要条件B.是的充分不必要条件C.是的必要不充分条件D.是的既不充分也不必...
- 在△ABC中,“”是“△ABC为钝角三角形”的[ ]A、充分不必要条件B、必要不充分条件C、充要条件D、既不充分又不必要条件
- 已知在△ABC中,角A,B,C的对边分别为a,b,c,且角A,B,C成等差数列,若边a,b,c成等比数列,求sinA•sinC的值.
- 在△ABC中,角A,B,C所对的边分别为a,b,c,已知a=2,b=22.(1)若∠C=45°,求c的值;(2)若∠A=30°,求∠B的值.
- 甲船在A处遇险,在甲船西南10海里B处的乙船收到甲船的报警后,测得甲船是沿着东偏北105°的方向,以每小时9海里的速度向某岛靠...