本试题 “有下列四个命题:①函数y=10-x和函数y=10x的图象关于x轴对称;②所有幂函数的图象都经过点(1,1);③若实数a、b满足a+b=1,则1a+4b的最小值为9;④若{an}是首项...” 主要考查您对真命题、假命题
充分条件与必要条件
指数函数的图象与性质
幂函数
基本不等式及其应用
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 真命题、假命题
- 充分条件与必要条件
- 指数函数的图象与性质
- 幂函数
- 基本不等式及其应用
命题的概念:
1、命题:把语言、符号或式子表达的,可以判断真假的陈述句称为命题;
2、真命题、假命题:判断为真的语句称为真命题,判断为假的语句称为假命题。
注意:
1、并不是所有的语句都是命题,只有能够判断真假的语句才是命题。
2、如果一个语句是命题,则它是真命题或是假命题,二者必具其一。
1、充分条件与必要条件:一般地,“若p,则q”为真命题,是指由p通过推理可以得出q,这时,我们就说,由p可推出q,记作 ,并且说p是q的充分条件,q是p的必要条件;
,并且说p是q的充分条件,q是p的必要条件;
2、充要条件:一般地,如果既有 ,又有
,又有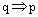 ,就记作
,就记作 ,此时,我们说,p是q的充分必要条件,简称充要条件。
,此时,我们说,p是q的充分必要条件,简称充要条件。
概括的说,如果 ,那么p与q互为充要条件。
,那么p与q互为充要条件。
3、充分不必要条件、必要不充分条件、既不充分也不必要条件:
①充分不必要条件:如果 ,且p
,且p q,则说p是q的充分不必要条件;
q,则说p是q的充分不必要条件;
②必要不充分条件:如果p q,且
q,且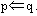 ,则说p是q的必要不充分条件;
,则说p是q的必要不充分条件;
③既不充分也不必要条件:如果p q,且p
q,且p q,则说p是q的既不充分也不必要条件。
q,则说p是q的既不充分也不必要条件。
指数函数y=ax(a>0,且a≠1)的图象和性质:
| 0<a<1 | a>1 | ||
| 图像 | 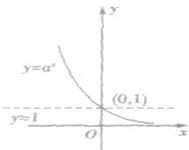 |
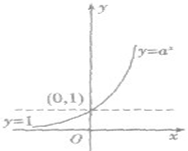 | |
| 图像 | 定义域 | R | |
| 值域 | (0,+∞) | ||
| 恒过定点 | 图像恒过定点(0,1),即当x等于0时,y=1 | ||
| 单调性 | 在(-∞,+∞)上是减函数 | 在(-∞,+∞)上是增函数 | |
| 函数值的变化规律 | 当x<0时,y>1 | 当x<0时,0<y<1 | |
| 当x=0时,y=1 | 当x=0时,y=1 | ||
| 当x>0时,0<y<1 | 当x>0时,y>1 | ||
底数对指数函数的影响:
①在同一坐标系内分别作函数的图象,易看出:当a>l时,底数越大,函数图象在第一象限越靠近y轴;同样地,当0<a<l时,底数越小,函数图象在第一象限越靠近x轴.
②底数对函数值的影响如图.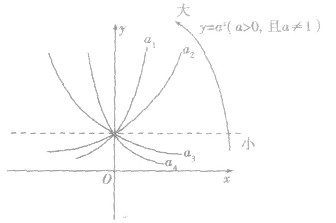
③当a>0,且a≠l时,函数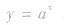 与函数y=
与函数y=![]() 的图象关于y轴对称。
的图象关于y轴对称。
利用指数函数的性质比较大小:
若底数相同而指数不同,用指数函数的单调性比较:
若底数不同而指数相同,用作商法比较;
若底数、指数均不同,借助中间量,同时要注意结合图象及特殊值,
指数函数图象的应用:
函数的图象是直观地表示函数的一种方法.函数的很多性质,可以从图象上一览无余.数形结合就是几何与代数方法紧密结合的一种数学思想.指数函数的图象通过平移、翻转等变可得出一般函数的图象.利用指数函数的图象,可解决与指数函数有关的比较大小、研究单调性、方程解的个数、求值域或最值等问题.
冥函数的定义:
一般地,函数y=xα叫做幂函数,其中x是自变量,α是常数。
幂函数的解析式:
y=xα
幂函数的图像:
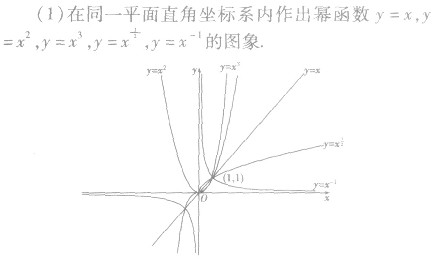
幂函数图像的性质:
所有幂函数在(0,+∞)上都有定义.
①α>0,图像都过定点(0,0)和(1,1);在区间(0,+∞)上单调递增;
②α<0,图像都过定点(1,1);在区间(0,+∞)上单调递减;
③当O<a<l时,曲线上凸,当a>l时,曲线下凸.
④当a=l时,图象为过点(0,0)和(1,1)的直线.
⑤当a=0时, 表示过点(1,1)且平行于x轴的直线(除去点(0,1)) 。
表示过点(1,1)且平行于x轴的直线(除去点(0,1)) 。
幂函数图象的其他性质:
(1)图象的对称性:
把幂函数 的幂指数a(只讨论a是有理数的情况)表示成既约分数的形式(整数看作是分母1的分数),则不论a>0还是a<0,幂函数
的幂指数a(只讨论a是有理数的情况)表示成既约分数的形式(整数看作是分母1的分数),则不论a>0还是a<0,幂函数 的图象的对称性用口诀记为:“子奇母偶孤单单;母奇子偶分两边;分子分母均为奇,原点对称莫忘记”,
的图象的对称性用口诀记为:“子奇母偶孤单单;母奇子偶分两边;分子分母均为奇,原点对称莫忘记”,
(2)图象的形状:
①若a>0,则幂函数 的图象为抛物线形,当a>l时,图象在[0,+∞)上是向下凸的(称为凸函数);当O<a<l时,图象在[o,+∞)上是向上凸的(称为凹函数).
的图象为抛物线形,当a>l时,图象在[0,+∞)上是向下凸的(称为凸函数);当O<a<l时,图象在[o,+∞)上是向上凸的(称为凹函数).
②若a<0,则幂函数y=x“的图象是双曲线形,图象与x轴、y轴无限接近,在(0,+∞)上图象都是向下凸的。
幂函数的单调性和奇偶性:
对于幂函数 (a∈R).
(a∈R).
(1)单调性
当a>0时,函数 在第一象限内是增函数;当a<0时,函数
在第一象限内是增函数;当a<0时,函数 在第一象限内是减函数.
在第一象限内是减函数.
(2)奇偶性
①当a为整数时,
若a为偶数,则 是偶函数;若a为奇数,则
是偶函数;若a为奇数,则 是奇函数。
是奇函数。
②当n为分数,即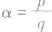 (p,q互素,p,q∈Z)时,若分母q为奇数,则分子p为奇数时,
(p,q互素,p,q∈Z)时,若分母q为奇数,则分子p为奇数时, 为奇函数;分子p为偶数时,
为奇函数;分子p为偶数时, 为偶函数, 若分母q为偶数,则
为偶函数, 若分母q为偶数,则 为非奇非偶函数.
为非奇非偶函数.
基本不等式:
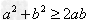 (当且仅当a=b时取“=”号);
(当且仅当a=b时取“=”号);
变式:①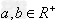 ,
,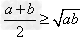 (当且仅当a=b时取“=”号),即两个正数的算术平均不小于它们的几何平均。
(当且仅当a=b时取“=”号),即两个正数的算术平均不小于它们的几何平均。
②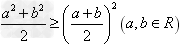 ;③
;③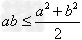 ;④
;④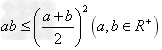 ;
;
对基本不等式的理解:
(1)基本不等式的证明是利用重要不等式推导的,即 ,即有
,即有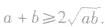
(2)基本不等式又称为均值定理、均值不等式等,其中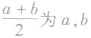 的算术平均数,
的算术平均数,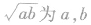 的几何平均数,本定理也可叙述为:两个正数的算术平均数不小于它们的几何平均数.
的几何平均数,本定理也可叙述为:两个正数的算术平均数不小于它们的几何平均数.
(3)要特别注意不等式成立的条件和等号成立的条件.均值不等式中:①当a=b时取等号,即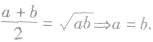
对于两个正数x,y,若已知xy,x+y,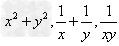 中的某一个为定值,可求出其余各个的最值:
中的某一个为定值,可求出其余各个的最值:
如:(1)当xy=P(定值),那么当x=y时,和x+y有最小值2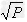 ,
,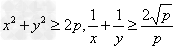 ;
;
(2)x+y=S(定值),那么当x=y时,积xy有最大值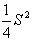 ,
,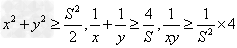 ;
;
(3)已知x2+y2=p,则x+y有最大值为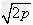 ,
, 。
。
应用基本的不等式解题时:
注意创设一个应用基本不等式的情境及使等号成立的条件,即“一正、二定、三相等”。
利用基本不等式比较实数大小:
(1)注意均值不等式的前提条件.
(2)通过加减项的方法配凑成使用均值定理的形式.
(3)注意“1”的代换.
(4)灵活变换基本不等式的形式,并注重其变形形式的运用.重要不等式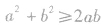 的形式可以是
的形式可以是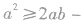
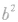 ,也可以是
,也可以是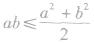 ,还可以是
,还可以是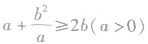 等,不仅要掌握原来的形式,还要掌握它的几种变形形式以及公式的逆用等,以便应用.
等,不仅要掌握原来的形式,还要掌握它的几种变形形式以及公式的逆用等,以便应用.
(5)合理配组,反复应用均值不等式。

与“有下列四个命题:①函数y=10-x和函数y=10x的图象关于x轴对称;...”考查相似的试题有:
- 设条件;条件,那么是的( ) 条件 A.充分非必要B.必要非充分C.充分且必要D.非充分非必要
- 下列命题:①x∈R,x2≥x;②x∈R,x2≥x;③4≥3;④“x2≠1”的充要条件是“x≠1,或x≠﹣1”.其中正确命题的个数是 [ ]A.0B.1C.2D.3
- (本小题满分10分)已知p:≤2,q:x2-2x+1-m2≤0(m>0),若非p是非q的必要不充分条件,求实数m的取值范围.
- 已知下列几个命题: ①已知F1、F2为两定点,=4,动点M满足,则动点M的轨迹是椭圆。 ②一个焦点为且与双曲线有相同的渐近线的双...
- 已知非零向量a、b及平面α,若向量a 是平面α的法向量,则a·b=0 是b所在直线平行于α或在α内的[ ]A.充分必要条件B.充分不必要...
- 设a∈R,则a>1是1a<1的( )A.既不充分也不必要条件B.必要但不充分条件C.充要条件D.充分但不必要条件
- 有下列五个命题:①“若x+y=0,则x,y互为相反数”的逆命题;②在平面内,F1、F2是定点,|F1F2|=6,动点M满足|MF1|-|MF2|=4|,则...
- 设x是实数,则“x>-1”是“|x|<1”的( )A.充分而不必要条件B.必要而不充分条件C.充要条件D.既不充分也不必要条件
- 函数f(x)=ax-1+2(a>0,a≠1)的图象恒过定点______.
- 幂函数y=xα(α≠0),当α取不同的正数时,在区间[0,1]上它们的图象是一簇美丽的曲线(如图),设点A(1,0),B(0,1),连结AB,线...