本试题 “已知O为坐标原点,M(cosx,23),N(2cosx,sinxcosx+36a)其中x∈R,a为常数,设函数f(x)=OM•ON(Ⅰ)求函数y=f(x)的表达式和对称轴方程;(Ⅱ)若角C为△ABC的三...” 主要考查您对已知三角函数值求角
正弦、余弦函数的图象与性质(定义域、值域、单调性、奇偶性等)
两角和与差的三角函数及三角恒等变换
向量数量积的运算
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 已知三角函数值求角
- 正弦、余弦函数的图象与性质(定义域、值域、单调性、奇偶性等)
- 两角和与差的三角函数及三角恒等变换
- 向量数量积的运算
反三角函数的定义:
(1)反正弦:在闭区间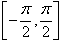 上符合条件sinx=a(-1≤a≤1)的角x,叫做实数a的反正弦,记作arcsina,即x=arcsina,其中x∈
上符合条件sinx=a(-1≤a≤1)的角x,叫做实数a的反正弦,记作arcsina,即x=arcsina,其中x∈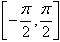 ,且a=sinx;
,且a=sinx;
注意arcsina表示一个角,这个角的正弦值为a,且这个角在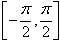 内(-1≤a≤1)。
内(-1≤a≤1)。
(2)反余弦:在闭区间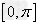 上,符合条件cosx=a(-1≤a≤1)的角x,叫做实数a的反余弦,记作arccosa,即x=arccosa,其中x∈[0,π],且a=cosx。
上,符合条件cosx=a(-1≤a≤1)的角x,叫做实数a的反余弦,记作arccosa,即x=arccosa,其中x∈[0,π],且a=cosx。
(3)反正切:在开区间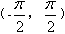 内,符合条件tanx=a(a为实数)的角x,叫做实数a的反正切,记做arctana,即x=arctana,其中x∈
内,符合条件tanx=a(a为实数)的角x,叫做实数a的反正切,记做arctana,即x=arctana,其中x∈ ,且a=tanx。
,且a=tanx。
反三角函数的性质:
(1)sin(arcsina)=a(-1≤a≤1),cos(arccosa)=a(-1≤a≤1),
tan(arctana)=a;
(2)arcsin(-a)=-arcsina,arccos(-a)=π-arccosa,arctan(-a)=-arctana;
(3)arcsina+arccosa=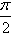 ;
;
(4)arcsin(sinx)=x,只有当x在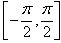 内成立;同理arccos(cosx)=x只有当x在闭区间[0,π]上成立。
内成立;同理arccos(cosx)=x只有当x在闭区间[0,π]上成立。
已知三角函数值求角的步骤:
(1)由已知三角函数值的符号确定角的终边所在的象限(或终边在哪条坐标轴上);
(2)若函数值为正数,先求出对应锐角α1,若函数值为负数,先求出与其绝对值对应的锐角α1;
(3)根据角所在象限,由诱导公式得出0~2π间的角,如果适合条件的角在第二象限,则它是π-α1;如果适合条件的角在第三象限,则它是π+α1;在第四象限,则它是2π-α1;如果是-2π到0的角,在第四象限时为-α1,在第三象限为-π+α1,在第二象限为-π-α1;
(4)如果要求适合条件的所有角,则利用终边相同的角的表达式来写出。
正弦函数和余弦函数的图象:正弦函数y=sinx(x∈R)和余弦函数y=cosx(x∈R)的图象分别叫做正弦曲线和余弦曲线,
1.正弦函数 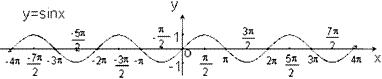
2.余弦函数
函数图像的性质
正弦、余弦函数图象的性质: 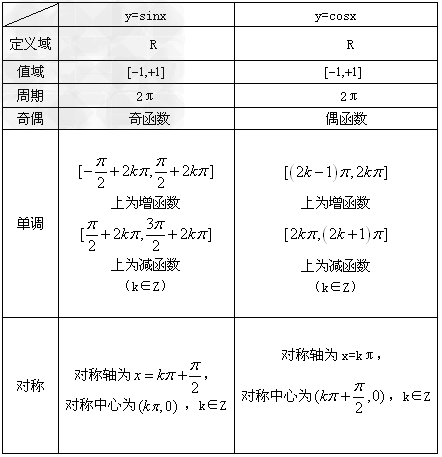
由上表知,正弦与余弦函数的定义域都是R,值域都是[-1,1],对y=sinx,当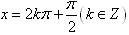 时,y取最大值1,
时,y取最大值1,
当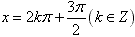 时,y取最小值-1;对y=cosx,当x=2kπ(k∈Z)时,y取最大值1,当x=2kπ+π(k∈Z)时,y取最小值-1。
时,y取最小值-1;对y=cosx,当x=2kπ(k∈Z)时,y取最大值1,当x=2kπ+π(k∈Z)时,y取最小值-1。
正弦、余弦函数图象的性质:

由上表知,正弦与余弦函数的定义域都是R,值域都是[-1,1],对y=sinx,当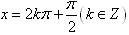 时,y取最大值1,
时,y取最大值1,
当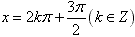 时,y取最小值-1;对y=cosx,当x=2kπ(k∈Z)时,y取最大值1,当x=2kπ+π(k∈Z)时,y取最小值-1。
时,y取最小值-1;对y=cosx,当x=2kπ(k∈Z)时,y取最大值1,当x=2kπ+π(k∈Z)时,y取最小值-1。
两角和与差的公式:
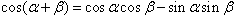
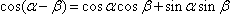
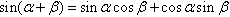
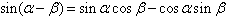
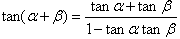
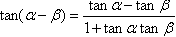
倍角公式:
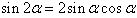
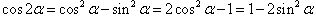
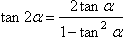
半角公式:
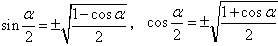
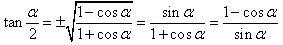
万能公式:
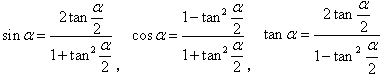
三角函数的积化和差与和差化积:
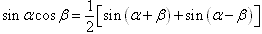

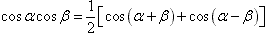
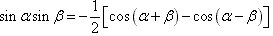
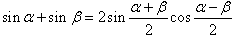
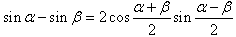
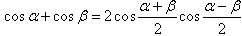
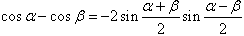
三角恒等变换:
寻找式子所包含的各个角之间的联系,并以此为依据选择可以联系它们的适当公式,这是三角恒等变换的特点。
三角函数式化简要遵循的"三看"原则:
(1)一看"角".这是最重要的一点,通过角之间的关系,把角进行合理拆分与拼凑,从而正确使用公式.
(2)二看"函数名称".看函数名称之间的差异,从而确定使用的公式.
(3)三看"结构特征".分析结构特征,可以帮助我们找到变形得方向,常见的有"遇到分式要通分"等.
方法提炼:
(1)解决给值求值问题的一般思路:
①先化简需求值得式子;②观察已知条件与所求值的式子之间的联系(从三角函数名及角入手);③将已知条件代入所求式子,化简求值.
(2)解决给值求角问题的一般步骤:
①求出角的某一个三角函数值;②确定角的范围;③根据角的范围确定所求的角.
两个向量数量积的含义:
如果两个非零向量 ,
, ,它们的夹角为
,它们的夹角为 ,我们把数量
,我们把数量 叫做
叫做 与
与 的数量积(或内积或点积),记作:
的数量积(或内积或点积),记作: ,即
,即 。
。 叫
叫 在
在 上的投影。
上的投影。
规定:零向量与任一向量的数量积是0,注意数量积是一个实数,不再是一个向量。
数量积的的运算律:
已知向量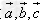 和实数λ,下面(1)(2)(3)分别叫做交换律,数乘结合律,分配律。
和实数λ,下面(1)(2)(3)分别叫做交换律,数乘结合律,分配律。
(1)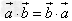 ;
;
(2)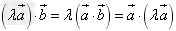 ;
;
(3)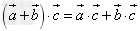 。
。
向量数量积的性质:
设两个非零向量
(1) ;
;
(2) ;
;
(3) ;
;
(4) ;
;
(5)当 ,
, 同向时,
同向时, ;当
;当 与
与 反向时,
反向时, ;当
;当 为锐角时,
为锐角时, 为正且
为正且 ,
, 不同向,
不同向, ;当
;当 为钝角时,
为钝角时, 为负且
为负且 ,
, 不反向,
不反向, 。
。
与“已知O为坐标原点,M(cosx,23),N(2cosx,sinxcosx+36a)其中x...”考查相似的试题有:
- 将函数的图象上所有点的横坐标伸长到原来的倍(纵坐标不变),再将所得的图象向左平移个单位,得到的图象对应的解析式是( )...
- (13分)已知函数()的最小正周期为.(1)求的值;(2)求函数在区间上的取值范围.
- cos750cos150- sin750sin150的值是( )A.B.-C.D.0
- (本题满分12分)已知,求:(1)的值; (2)的值.
- 设A是单位圆和x轴正半轴的交点,P,Q是单位圆上两点,O是坐标原点,且∠AOP=π6,∠AOQ=α,α∈[0,π).(Ⅰ)若点Q的坐标是 (m,...
- 设sin,则( )A.B.C.D.
- (2013•盐城三模)已知α,β∈(0,π),且tanα=2,cosβ=-7210.(1)求cos2α的值;(2)求2α-β的值.
- 已知, 求的值。
- 已知D是△ABC所在平面上任意一点,若(AB-BC)•(AD-CD)=0,则△ABC一定是( )A.直角三角形B.等腰直角三角形C.等腰三角形D...
- 已知椭圆C:x2a2+y2b2=1(a>b>0)的焦距为23,离心率为22,其右焦点为F,过点B(0,b)作直线交椭圆于另一点A.(Ⅰ)若AB•BF=...