本试题 “已知集合A是函数y=lg(20+8x-x2)的定义域,集合B是不等式x2-2x+1-a2≥0(a>0)的解集,p:x∈A,q:x∈B,(Ⅰ)若A∩B=∅,求a的取值范围;(Ⅱ)若¬p是q的充分不...” 主要考查您对集合间交、并、补的运算(用Venn图表示)
四种命题及其相互关系
充分条件与必要条件
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 集合间交、并、补的运算(用Venn图表示)
- 四种命题及其相互关系
- 充分条件与必要条件
1、交集概念:
(1)一般地,由所有属于集合A且集合B的元素所组成的集合,叫做A与B的交集,记作A∩B,读作A交B,表达式为A∩B={x|x∈A且x∈B}。
(2)韦恩图表示为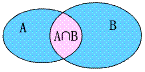 。
。
2、并集概念:
(1)一般地,由所有属于集合A或集合B的元素所组成的集合,叫做A与B的并集,记作A∪B,读作A并B,表达式为A∪B={x|x∈A或x∈B}。
(2)韦恩图表示为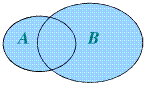 。
。
3、全集、补集概念:
(1)全集:一般地,如果一个集合含有我们所要研究的各个集合的全部元素,就称这个集合为全集,通常记作U。
补集:对于一个集合A,由全集U中所有不属于A的元素组成的集合称为集合A相对于全集U的补集,记作CUA,读作U中A的补集,表达式为CUA={x|x∈U,且x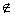 A}。
A}。
(2)韦恩图表示为 。
。
1、交集的性质:
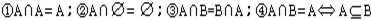
2、并集的性质:
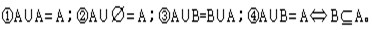
3、补集的性质:
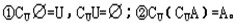
1、四种命题:
一般地,用p和q分别表示原命题的条件和结论,用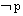 或
或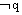 分别表示p和q的否定,
分别表示p和q的否定,
四种命题的形式是:
(1)原命题:若p则q;
(2)逆命题:若q则p;
(3)否命题:若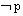 则
则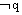 ;
;
(4)逆否命题:若 则
则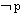 。
。
2、四种命题的真假关系:
一个命题与它的逆否命题是等价的,其逆命题与它的否命题也是等价的;
3、四种命题的相互关系:
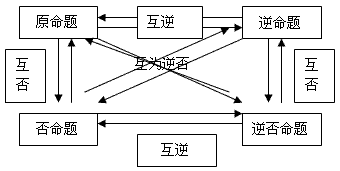
注意:
1、区别“否命题”与“命题的否定”,若原命题是“若p则q”,则这个命题的否定是“若p则非q”,而它的否命题是“若非p则非q”。
2、互为逆否命题同真假,即“等价”
1、充分条件与必要条件:一般地,“若p,则q”为真命题,是指由p通过推理可以得出q,这时,我们就说,由p可推出q,记作 ,并且说p是q的充分条件,q是p的必要条件;
,并且说p是q的充分条件,q是p的必要条件;
2、充要条件:一般地,如果既有 ,又有
,又有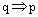 ,就记作
,就记作 ,此时,我们说,p是q的充分必要条件,简称充要条件。
,此时,我们说,p是q的充分必要条件,简称充要条件。
概括的说,如果 ,那么p与q互为充要条件。
,那么p与q互为充要条件。
3、充分不必要条件、必要不充分条件、既不充分也不必要条件:
①充分不必要条件:如果 ,且p
,且p q,则说p是q的充分不必要条件;
q,则说p是q的充分不必要条件;
②必要不充分条件:如果p q,且
q,且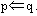 ,则说p是q的必要不充分条件;
,则说p是q的必要不充分条件;
③既不充分也不必要条件:如果p q,且p
q,且p q,则说p是q的既不充分也不必要条件。
q,则说p是q的既不充分也不必要条件。
与“已知集合A是函数y=lg(20+8x-x2)的定义域,集合B是不等式x2-...”考查相似的试题有:
- 已知集合P、Q、M满足P∩Q=P,Q∩M=Q,则P、M的关系为( )A.PMB.PMC.PMD.PM
- 若,求a的取值范围
- 集合,,若,则的值为( )A. 0B.1C.2D.4
- 若集合,则满足条件有 个.
- (本题满分12分)已知集合,实数使得集合满足,求的取值范围.
- 设集全A=则集合A∩B=( )A.{0,1,2}B.{0,1,2,3}C.{0,1,3}D.B
- 设数列{an}、{bn}、{cn}满足:bn=an-an+2,cn=an+2an+1+3an+2(n=1,2,3,…),证明:{an}为等差数列的充分必要条件是{cn}为...
- “”是“”的A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件
- 下列命题中,假命题为( )A.存在四边相等的四边形不是正方形B.z1,z2∈C,z1+z2为实数的充分必要条件是z1,z2互为共轭复数C...
- 已知条件,条件q:,则p是q的[ ]A.充分非必要条件B.必要非充分条件C.充要条件D.既不充分也不必要条件