本试题 “已知函数f(x)=-12x22x,g(x)=logax(a>0,且a≠1),其中a为常数.如果h(x)=f(x)+g(x)是增函数,且h′(x)存在零点(h′(x)为h(x)的导函数)....” 主要考查您对函数的零点与方程根的联系
导数的运算
函数的单调性与导数的关系
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 函数的零点与方程根的联系
- 导数的运算
- 函数的单调性与导数的关系
函数零点的定义:
一般地,如果函数y =f(x)在实数a处的值等于零,即f(a)=o,则a叫做这个函数的零点,有时我们把一个函数的图象与x轴的交点的横坐标,也叫做这个函数的零点。
函数零点具有的性质:
对于任意函数y=(x)只要它的图象是连续不间断的,则有:
(1)当它通过零点时(不是二重零点),函数值变号.如函数f(x)=x2-2x -3的图象在零点-1的左边时,函数值取正号,当它通过第一个零点-1时,函数值由正变为负,在通过第二个零点3时,函数值又由负变为正.
(2)在相邻两个零点之间所有的函数值保持同号,
方程的根与函数的零点的联系:
方程f(x)=0有实根 函数y=f(x)的图像与x轴有交点
函数y=f(x)的图像与x轴有交点 函数y=f(x)有零点
函数y=f(x)有零点
常见函数的导数:
(1)C′=0 ;(2)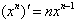 ;(3)
;(3)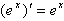 ;(4)
;(4) ;(5)
;(5)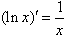 ;(6)
;(6)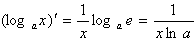 ;(7)
;(7)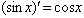 ;(8)
;(8)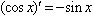
导数的四则运算:
(1)和差: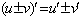
(2)积: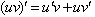
(3)商:
复合函数的导数:
运算法则复合函数导数的运算法则为: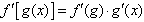
复合函数的求导的方法和步骤:
(1)分清复合函数的复合关系,选好中间变量;
(2)运用复合函数求导法则求复合函数的导数,注意分清每次是哪个变量对哪个变量求导数;
(3)根据基本函数的导数公式及导数的运算法则求出各函数的导数,并把中间变量换成自变量的函数。
求复合函数的导数一定要抓住“中间变量”这一关键环节,然后应用法则,由外向里一层层求导,注意不要漏层。
导数和函数的单调性的关系:
(1)若f′(x)>0在(a,b)上恒成立,则f(x)在(a,b)上是增函数,f′(x)>0的解集与定义域的交集的对应区间为增区间;
(2)若f′(x)<0在(a,b)上恒成立,则f(x)在(a,b)上是减函数,f′(x)<0的解集与定义域的交集的对应区间为减区间。
利用导数求解多项式函数单调性的一般步骤:
①确定f(x)的定义域;
②计算导数f′(x);
③求出f′(x)=0的根;
④用f′(x)=0的根将f(x)的定义域分成若干个区间,列表考察这若干个区间内f′(x)的符号,进而确定f(x)的单调区间:f′(x)>0,则f(x)在对应区间上是增函数,对应区间为增区间;f′(x)<0,则f(x)在对应区间上是减函数,对应区间为减区间。
函数的导数和函数的单调性关系特别提醒:
若在某区间上有有限个点使f′(x)=0,在其余的点恒有f′(x)>0,则f(x)仍为增函数(减函数的情形完全类似).即在区间内f′(x)>0是f(x)在此区间上为增函数的充分条件,而不是必要条件。
与“已知函数f(x)=-12x22x,g(x)=logax(a>0,且a≠1),其中...”考查相似的试题有:
- 已知为R上的连续可导函数,当时,,则关于的函数的零点的个数为 A.1 B.2C.D.或
- 如果关于x的方程|x|x+4=kx2有4个不同的实数解,则实数k的取值范围是( )A.(0,14)B.(14,1)C.(1,+∞)D.(14,+∞)
- 已知f1(x)=sinx+cosx,记f2(x)=f1′(x),f3(x)=f2′(x),…,fn(x)=fn-1′(x),(n∈N*,n≥2),则f1(π2)+f2(π2)+…+f2012(π2)=____...
- 已知函数.(Ⅰ)若曲线y=f(x)在x=1和x=3处的切线互相平行,求a的值;(Ⅱ)求f(x)的单调区间;(Ⅲ)设g(x)=x2﹣2x,若对...
- 已知函数y=f(x)的图象关于y轴对称,且当x∈(-∞,0)时,f(x)+xf′(x)<0成立,a=(20.2)·f(20.2),b=(logπ3)·f(logπ3),c=(...
- 设函数f(x)=x2-ax+aex.(1)当a=0时,求曲线y=f(x)在点(1,f(1)处的切线方程;(2)讨论f(x)的单调性.
- 设a>0,函数f(x)=x-ax2+1+a.(I)若f(x)在区间(0,1]上是增函数,求a的取值范围;(Ⅱ)求f(x)在区间(0,1]上的最大值.
- 已知函数y=f(x)(x∈R)在任一点(x0,f(x0))处的切线斜率为k=(x0-2)(x0+1)2,则该函数的单调递减区间为______.
- 定义域R的奇函数f(x),当x∈(-∞,0)时f(x)+xf′(x)<0恒成立,若a=3f(3),b=f(1),c=-2f(-2),则( )A.a>c>b...
- 已知函数f(x)=13x3-12(a+1)x2+ax,g(x)=f′(x)是函数f(x)的导函数,其中实数a是不等1的常数.(1)设a>1,讨论函数...