本试题 “若|a|=2,且(a-b)⊥a,则a•b=______.” 主要考查您对用数量积判断两个向量的垂直关系
向量数量积的运算
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 用数量积判断两个向量的垂直关系
- 向量数量积的运算
两向量垂直的充要条件:
非零向量 ,那么
,那么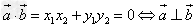 ,所以可以根据此公式判断两个向量是否垂直。
,所以可以根据此公式判断两个向量是否垂直。
向量数量积的性质:
设两个非零向量
(1) ;
;
(2) ;
;
(3) ;
;
(4) ;
;
(5)当 ,
, 同向时,
同向时, ;当
;当 与
与 反向时,
反向时, ;当
;当 为锐角时,
为锐角时, 为正且
为正且 ,
, 不同向,
不同向, ;当
;当 为钝角时,
为钝角时, 为负且
为负且 ,
, 不反向,
不反向, 。
。
两个向量数量积的含义:
如果两个非零向量 ,
, ,它们的夹角为
,它们的夹角为 ,我们把数量
,我们把数量 叫做
叫做 与
与 的数量积(或内积或点积),记作:
的数量积(或内积或点积),记作: ,即
,即 。
。 叫
叫 在
在 上的投影。
上的投影。
规定:零向量与任一向量的数量积是0,注意数量积是一个实数,不再是一个向量。
数量积的的运算律:
已知向量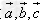 和实数λ,下面(1)(2)(3)分别叫做交换律,数乘结合律,分配律。
和实数λ,下面(1)(2)(3)分别叫做交换律,数乘结合律,分配律。
(1)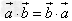 ;
;
(2)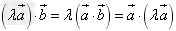 ;
;
(3)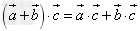 。
。
向量数量积的性质:
设两个非零向量
(1) ;
;
(2) ;
;
(3) ;
;
(4) ;
;
(5)当 ,
, 同向时,
同向时, ;当
;当 与
与 反向时,
反向时, ;当
;当 为锐角时,
为锐角时, 为正且
为正且 ,
, 不同向,
不同向, ;当
;当 为钝角时,
为钝角时, 为负且
为负且 ,
, 不反向,
不反向, 。
。
发现相似题
与“若|a|=2,且(a-b)⊥a,则a•b=______.”考查相似的试题有:
- 已知向量x=(1,t2-3 ),y=(-k,t) (其中实数k和t不同时为零),当|t|<2时,有x⊥y,当|t|>2时,有x∥y.(1)求函数关系...
- 平面向量a=(3,4),b=(2,x),c=(2,y),已知a∥b,a⊥c,求b,c及b与c夹角.
- 已知向量a=(2,x),b=(1,4),若a⊥b,则实数x的值为( ) A.8 B. C.- D.-2
- 在平面直角坐标系xOy中,圆C:x2+y2=4分别交x轴正半轴及y轴负半轴于M,N两点,点P为圆C上任意一点,则PM•PN的最大值为______.
- 已知⊙O:x2+y2=4及点A(1,3),BC为⊙O的任意一条直径,则=[ ]A.6B.5C.4D.不确定
- 在△ABC中,角A、B、C所对的边分别是a、b、c,且有bcosC=3acosB-ccosB。(1)求cosB的值;(2)若=2,b=2,求a和c的值。
- 在△ABC中,a,b,c分别为角A,B,C所对的边,向量m=(2a+c,b),n=(cosB,cosC),且m,n垂直.( I)确定角B的大小;( II...
- 已知向量a=(sinx+cosx,2),b=(1,sinxcosx),设f(x)=a•b,x∈[0,π2],求f(x)的值域.
- 若平面向量,,两两所成的角相等,||=||=1,||=3,则|++|=( ) A.2 B.4 C.2或5 D.4或5
- 已知△ABC内接于以O为圆心,1为半径的圆,且3OA+4OB+5OC=0(1)求数量积,OA•OB,OB•OC,OC•OA;(2)求△ABC的面积.