已知命题p：函数y=log0、5（x2+2x+a）的值域为R，命题q：函数y=-（5-2a）x是减函数、若p或q为真命题，p且q为假命题，则,高中,数学试题,真命题、假命题考点,指数函数模型的应用考点,对数函数的解析式及定义（定义域、值域）考点,好技网

填空题
已知命题p：函数y=log_0、5（x²+2x+a）的值域为R，命题q：函数y=-（5-2a）^x是减函数、若p或q为真命题，p且q为假命题，则实数a的取值范围是______、

本题信息：数学填空题难度一般来源:未知
本题答案
查看答案

本试题 “已知命题p：函数y=log0、5（x2+2x+a）的值域为R，命题q：函数y=-（5-2a）x是减函数、若p或q为真命题，p且q为假命题，则实数a的取值范围是______、” 主要考查您对
真命题、假命题

指数函数模型的应用

对数函数的解析式及定义（定义域、值域）
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。

真命题、假命题
指数函数模型的应用
对数函数的解析式及定义（定义域、值域）

命题的概念：

1、命题：把语言、符号或式子表达的，可以判断真假的陈述句称为命题；
2、真命题、假命题：判断为真的语句称为真命题，判断为假的语句称为假命题。

注意：

1、并不是所有的语句都是命题，只有能够判断真假的语句才是命题。

2、如果一个语句是命题，则它是真命题或是假命题，二者必具其一。

指数函数模型的定义：

恰当选择自变量将问题的目标表示成自变量的函数f（x）=a·b^x+c（a、b、c为常数，a≠0，b＞0，b≠1）的形式，进而结合指数函数的性质解决问题。

指数型复合函数的性质的应用:

(1)与指数函数有关的复合函数基本上有两类：
；②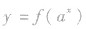.无论是哪一类，要搞清楚复合过程，才能确定复合函数的值域和单调区间，具体问题中，a的取值不定时，要对a进行分类讨论．
(2)对于形如一类的指数型复合函数，有以下结论：
①函数的定义域与f(x)的定义域相同；
②先确定函数f(x)的值域，再根据指数函数的值域、单调性，确定函数的值域；
③当a>l时，函数与函数f(x)的单调性相同；当O<a<l时，函数与函数f(x)的单调性相反.

对数函数的定义：

一般地，我们把函数y=log_ax（a＞0，且a≠1）叫做对数函数，其中x是自变量，函数的定义域是（0，+∞），值域是R。

对数函数的解析式：

y=log_ax（a＞0，且a≠1）

在解有关对数函数的解析式时注意：

在涉及到对数函数时，一定要注意定义域，即满足真数大于零；求值域时，还要考虑底数的取值范围。

发现相似题

与“已知命题p：函数y=log0、5（x2+2x+a）的值域为R，命题q：函数...”考查相似的试题有：