本试题 “已知向量m=(3sinx-cosx, 1),n=(cosx, 12),若f(x)=m•n.(1) 求函数f(x)的最小正周期;(2) 已知△ABC的三内角A、B、C的对边分别为a、b、c,且c=3, f(...” 主要考查您对已知三角函数值求角
任意角的三角函数
正弦定理
余弦定理
平面向量的应用
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 已知三角函数值求角
- 任意角的三角函数
- 正弦定理
- 余弦定理
- 平面向量的应用
反三角函数的定义:
(1)反正弦:在闭区间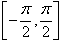 上符合条件sinx=a(-1≤a≤1)的角x,叫做实数a的反正弦,记作arcsina,即x=arcsina,其中x∈
上符合条件sinx=a(-1≤a≤1)的角x,叫做实数a的反正弦,记作arcsina,即x=arcsina,其中x∈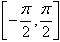 ,且a=sinx;
,且a=sinx;
注意arcsina表示一个角,这个角的正弦值为a,且这个角在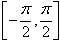 内(-1≤a≤1)。
内(-1≤a≤1)。
(2)反余弦:在闭区间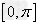 上,符合条件cosx=a(-1≤a≤1)的角x,叫做实数a的反余弦,记作arccosa,即x=arccosa,其中x∈[0,π],且a=cosx。
上,符合条件cosx=a(-1≤a≤1)的角x,叫做实数a的反余弦,记作arccosa,即x=arccosa,其中x∈[0,π],且a=cosx。
(3)反正切:在开区间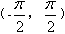 内,符合条件tanx=a(a为实数)的角x,叫做实数a的反正切,记做arctana,即x=arctana,其中x∈
内,符合条件tanx=a(a为实数)的角x,叫做实数a的反正切,记做arctana,即x=arctana,其中x∈ ,且a=tanx。
,且a=tanx。
反三角函数的性质:
(1)sin(arcsina)=a(-1≤a≤1),cos(arccosa)=a(-1≤a≤1),
tan(arctana)=a;
(2)arcsin(-a)=-arcsina,arccos(-a)=π-arccosa,arctan(-a)=-arctana;
(3)arcsina+arccosa=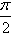 ;
;
(4)arcsin(sinx)=x,只有当x在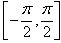 内成立;同理arccos(cosx)=x只有当x在闭区间[0,π]上成立。
内成立;同理arccos(cosx)=x只有当x在闭区间[0,π]上成立。
已知三角函数值求角的步骤:
(1)由已知三角函数值的符号确定角的终边所在的象限(或终边在哪条坐标轴上);
(2)若函数值为正数,先求出对应锐角α1,若函数值为负数,先求出与其绝对值对应的锐角α1;
(3)根据角所在象限,由诱导公式得出0~2π间的角,如果适合条件的角在第二象限,则它是π-α1;如果适合条件的角在第三象限,则它是π+α1;在第四象限,则它是2π-α1;如果是-2π到0的角,在第四象限时为-α1,在第三象限为-π+α1,在第二象限为-π-α1;
(4)如果要求适合条件的所有角,则利用终边相同的角的表达式来写出。
任意角的三角函数的定义:
设α是任意一个角,α的终边上任意一点P的坐标是(x,y),它与原点的距离是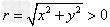 ,那么
,那么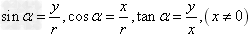 ,
,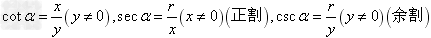 ,
,
以上以角为自变量,比值为函数的六个函数统称为三角函数。三角函数值只与角的大小有关,而与终边上点P的位置无关。
象限角的三角函数符号:
一全正,二正弦,三两切,四余弦。
特殊角的三角函数值:(见下表)
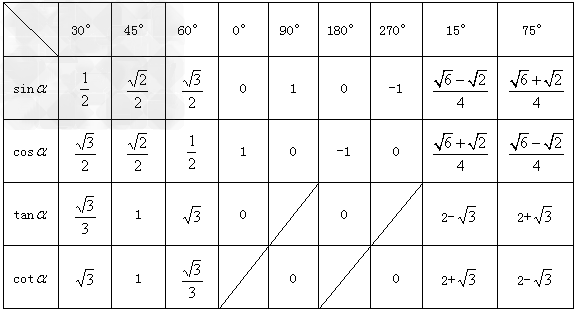
正弦定理:
在一个三角形中,各边和它所对角的正弦的比相等,即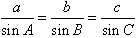 =2R。
=2R。
有以下一些变式:
(1)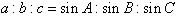 ;
;
(2)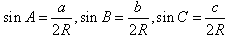 ;
;
(3)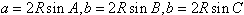 。
。
正弦定理在解三角形中的应用:
(1)已知两角和一边解三角形,只有一解。
(2)已知两边和其中一边的对角,解三角形,要注意对解的个数的讨论。可按如下步骤和方法进行:先看已知角的性质和已知两边的大小关系。
如已知a,b,A,
(一)若A为钝角或直角,当b≥a时,则无解;当a≥b时,有只有一个解;
(二)若A为锐角,结合下图理解。
①若a≥b或a=bsinA,则只有一个解。
②若bsinA<a<b,则有两解。
③若a<bsinA,则无解。 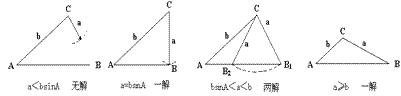
也可根据a,b的关系及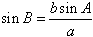 与1的大小关系来确定。
与1的大小关系来确定。
余弦定理:
三角形任意一边的平方等于其他两边的平方的和减去这两边与它们夹角的余弦的积的两倍,
即 。
。
推论:
在△ABC中,若a2+b2=c2,则C为直角;若a2+b2>c2,则C为锐角;若a2+b2<c2,则C为钝角。
余弦定理在解三角形中的应用:
(1)已知两边和夹角,
(2)已知三边。
其它公式:
射影公式: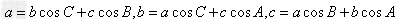
平面向量在几何、物理中的应用
1、向量在平面几何中的应用:
(1)证明线段相等平行,常运用向量加法的三角形法则、平行四边形法则,有时也用到向量减法的定义;
(2)证明线段平行,三角形相似,判断两直线(或线段)是否平行,常运用到向量共线的条件;
(3)证明垂直问题,常用向量垂直的充要条件;
1、向量在三角函数中的应用:
(1)以向量为载体研究三角函数中最值、单调性、周期等三角函数问题;
(2)通过向量的线性运算及数量积、共线来解决三角形中形状的判断、边角的大小与关系。
2、向量在物理学中的应用:
由于力、速度是向量,它们的分解与合成与向量的加法相类似,可以用向量方法来解决,力做的功就是向量中数量积的一种体现。
3、向量在解析几何中的应用:
(1)以向量为工具研究平面解析几何中的坐标、性质、长度等问题;
(2)以向量知识为工具研究解析几何中常见的轨迹与方程问题。
平面向量在几何、物理中的应用
1、用向量解决几何问题的步骤:
(1)建立平面几何与向量的联系,用向量表示问题中涉及的几何元素,将平面问题转化为向量问题;
(2)通过向量运算,研究几何元素之间的关系,如:距离,夹角等;
(3)把运算结果“翻译”成几何关系。
2、用向量中的有关知识研究物理中的相关问题,步骤如下:
(1)问题的转化,即把物理问题转化为数学问题;
(2)模型的建立,即建立以向量为主题的数学模型;
(3)求出数学模型的有关解;
(4)将问题的答案转化为相关的物理问题。
与“已知向量m=(3sinx-cosx, 1),n=(cosx, 12),若f(x)=m•n.(...”考查相似的试题有:
- 在△ABC中,角A,B,C的对边分别为a,b,c,其中c边最长,并且sin2A+sin2B=1,则△ABC的形状为______.
- 若,且,则 ( )A.B.C.D.
- 已知α是第二限角,则下列结论正确的是( ) A.sinα•cosα>0 B.sinα•tanα<0 C.cosα•tanα<0 D.以上都有可能
- 已知θ为锐角,则下列选项提供的各值中,可能为sinθ+cosθ的值的是( )A.43B.35C.45D.12
- 已知函数.(1)求的最小正周期;(2)求在区间上的最大值和最小值.(3)若g(x)=f(),求函数g(x)的单调增区间;
- △ABC中,角A,B,C所对的边分别为a,b,c,若acosA=bsinB,则sinAcosA+cos2B=______.
- 在△ABC中,内角A、B、C的对边分别为a、b、c,已知.(Ⅰ)求的值;(Ⅱ)若cosB=,b=2, 求△ABC的面积S.
- 在△ABC中,角A、B、C的对边分别为a、b、c,若(1)判断△ABC的形状;(2)若的值.
- 若对个向量,存在个不全为零的实数,使得=成立,则称向量为“线性相关”.依此规定,请你求出一组实数的值,它能说明="(1,0),"=(...
- 已知动点P(x,y)在椭圆x2 25+y2 24=1上,若A点坐标为(1,0),M是平面内任一点,|AM|=1,且PM•AM=0,则|PM|的最小值是( ...