向量加法的定义:
已知非零向量a,b,在平面内任取一点A,作 ,再做向量
,再做向量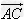 ,则向量
,则向量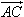 叫做
叫做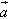 与
与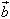 的和,即
的和,即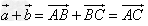 。
。
作向量的加法有“三角形法则”和“平行四边形法则”,其中“平行四边形法则”只适用于不共线的向量。
向量加法的三角形法则:
已知非零向量a,b,在平面内任意取一点A,作 a,
a,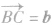 ,
,

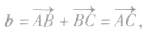
这种求向量和的方法称为向量加法的三角形法则,如图
向量加法的平行四边形法则:
以同一点O起点的两个已知向量
a,b为邻边作平行四边形OACB,则以O为起点的对角线OC就是
a与
b的和,这种作两个向量和的方法叫做向量加法的平行四边形法则,如图.
向量减法的定义:
向量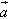 与向量
与向量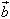 的相反向量的和,叫做向量
的相反向量的和,叫做向量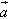 与向量
与向量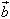 的差,记作:
的差,记作: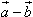 。
。
作向量减法有“三角形法则”:设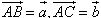 ,那么
,那么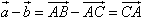 ,由减向量和终点指向被减向量和终点。
,由减向量和终点指向被减向量和终点。
注意:此处减向量与被减向量的起点相同。
向量减法的作图法:
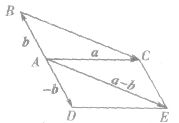
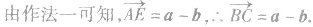
因此,
a-b可以表示为从向量
b的终点指向向量
a的终点的向量,这就是向量减法的几何意义.
坐标运算:
已知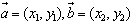 ,则
,则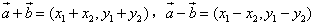 。
。
向量加减法的运算律:
(1)交换律: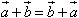 ;
;
(2)结合律: 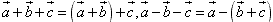
求向量的和的三角形法则的理解:
使用三角形法则特别要注意“首尾相接”,具体做法是把用小写字母表示的向量,用两个大写字母表示(其中后面向量的起点与其前一个向量的终点重合,即用同一个字母表示),则由第一个向量的起点指向最后一个向量终点的有向线段就表示这些向量的和。对于n个向量,仍有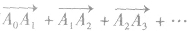
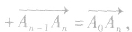 这可以称为向量加法的多边形法则。
这可以称为向量加法的多边形法则。
作两个向量的和向量,可分四步:
①取点,注意取点的任意性;
②作相等向量,分别作与两个已知向量相等的向量,使它们的起点重合;
③作平行四边形,以两个向量为邻边作平行四边形;
④作和向量,与两个向量有共同起点的对角线作为和向量,共同的起点作为和向量的起点,对角线的另一个端点作为和向量的终点.当两个向量不共线时,三角形法则和平行四边形法则是一致的;当两个向量共线时,三角形法则同样适用,而平行四边形法则就不适用了.
向量的加法需要说明的几点:
①当两个非零向量a与b不共线时,a+b的方向与a,b的方向都不相同,且
②当两个非零向量a与b共线时,
a.向量a与b同向(如下图),即向量a+b与a(或b)方向相同,且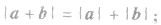

b.向量a与b反向(如上图)且|a|<|b|时,即a+b与b方向相同(与a方向相反),且
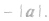
综上可知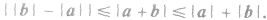
向量减法的理解:
①定义向量减法是借助了相反向量和向量加法,其实,向量减法的实质是向量加法的逆运算.两个向量的差仍是向量;
②作差向量时,作法一较为复杂,作法二较为简捷,应根据问题的需要灵活运用;
③以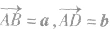 为邻边作平行四边形ABCD,则两条对角线表示的向量为
为邻边作平行四边形ABCD,则两条对角线表示的向量为 这一结论在以后的应用是非常广泛的,应该加强理解并记住;
这一结论在以后的应用是非常广泛的,应该加强理解并记住;
④对于任意一点O,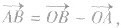 简记为“中减起”,在解题中经常用到,必须记住.
简记为“中减起”,在解题中经常用到,必须记住.
向量共线的充要条件:
向量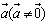 与
与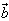 共线,当且仅当有唯一一个实数λ,使得
共线,当且仅当有唯一一个实数λ,使得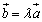 。
。
向量共线的几何表示:
设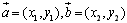 ,其中
,其中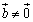 ,当且仅当
,当且仅当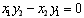 时,向量
时,向量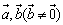 共线。
共线。
向量共线(平行)基本定理的理解:
(1)对于向量a(a≠0),b,如果有一个实数λ,使得b=λa,那么由向量数乘的定义知,a与b共线.
(2)反过来,已知向量a与b共线,a≠0,且向量b的长度是向量a的长度的μ倍,即|b|=μ|a|,那么当a与b同方向时,有b=μa;当a与b反方向时,有b=-μa.
(3)向量平行与直线平行是有区别的,直线平行不包括重合.
(4)判断a(a≠0)与b是否共线时,关键是寻找a前面的系数,如果系数有且只有一个,说明共线;如果找不到满足条件的系数,则这两个向量不共线.
(5)如果a=b=0,则数λ仍然存在,且此时λ并不唯一,是任意数值.
用数量积表示两个向量的夹角:
设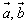 都是非零向量,
都是非零向量,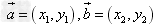 ,θ是
,θ是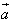 与
与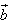 的夹角,根据向量数量积的定义及坐标表示可得
的夹角,根据向量数量积的定义及坐标表示可得
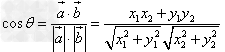 。
。
向量数量积问题中方法提炼:
(1)平面向量的数量积的运算有两种形式,一是依据定义来计算,二是利用坐标来计算,具体应用哪种形式应根据已知条件的特征来选择;
(2)平面向量数量积的计算类似于多项式的运算,解题中要注意多项式运算方法的运用;
(3)平面向量数量积的计算中要注意平面向量基本定理的应用,选择合适的基底,以简化运算
(4)向量的数量积是一个数而不是一个向量。