本试题 “(几何证明选讲)如图,点A、B、C都在⊙O上,过点C的切线交AB的延长线于点D,若AB=5,BC=3,CD=6,则线段AC的长为______.” 主要考查您对相似三角形的判定及有关性质
弦切角的性质
与圆有关的比例线段
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 相似三角形的判定及有关性质
- 弦切角的性质
- 与圆有关的比例线段
相似三角形的定义:
对应角相等,对应边成比例的两个三角形叫做相似三角形。相似三角形对应边的比值叫做相似比(或相似系数)。
预备定理:
平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与三角形相似
判定定理1:
对于任意两个三角形,如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似。简述为:两角对应相等,两三角形相似。
判定定理2:
对于任意两个三角形,如果一个三角形的两边和另一个三角形的两边对应成比例,并且夹角相等,那么这两个三角形相似。简述为:两边对应成比例且夹角相等,两三角形相似。
判定定理3:
对于任意两个三角形,如果一个三角形的三条边和另一个三角形的三条边对应成比例,那么这两个三角形相似。简述为:三边对应成比例,两三角形相似。
引理:
如果一条直线截三角形的两边(或两边的延长线)所得的对应线段成比例,那么这条直线平行于三角形的第三边。
直角三角形相似定理:
(1)如果两个直角三角形有一个锐角对应相等,那么它们相似;
(2)如果两个直角三角形的两条直角边对应成比例,那么它们相似。
(3)如果一个直角三角形的斜边和一条直角边与另一个三角形的斜边和直角边对应成比例,那么这两个直角三角形相似。
相似三角形的性质 :
(1)相似三角形对应高、中线、角平分线的比等于相似比;
(2)相似三角形周长的比等于相似比,相似三角形面积的比等于相似比的平方;
(3)相似三角形对应角相等,对应边成比例;
(4)相似三角形外接圆或内切圆的直径比、周长比等于相似比,外接圆或内切圆的面积等于相似比的平方。
相似三角形的判定方法 :
由于从定义出发判断两个三角形是否相似,需考虑6个元素,即三组对应角是否分别相等,三组对应边是否分别成比例,显然比较麻烦。所以我们曾经给出过如下几个判定两个三角形相似的简单方法:
(1)如果一个三角形的两条边与另一个三角形的两条边对应成比例,并且夹角相等,那么这两个三角形相似;
(2)如果一个三角形的三条边和另一个三角形的三条边对应成比例,那么这两个三角形相似;
(3)如果一个三角形的两个角和另一个三角形两个角对应相等,那么这两个三角形相似。
弦切角的定义:
顶点在圆上,一边和圆相交,另一边和圆相切的角叫做弦切角。(弦切角就是切线与弦所夹的角)
如图所示,直线PT切圆O于点C,BC、AC为圆O的弦,∠TCB、∠TCA、∠PCA、∠PCB都为弦切角。
弦切角定理:
弦切角等于它所夹的弧所对的圆周角;
弦切角的度数等于它所夹的弧的圆心角的度数的一半。
弦切角定理证明:
设圆心为O,连接OC,OB,
∵∠TCB=90°-∠OCB∵∠BOC=180°-2∠OCB∴,∠BOC=2∠TCB(定理:弦切角的度数等于它所夹的弧所对的圆心角的度数的一半)
∵∠BOC=2∠CAB(同一弧所对的圆心角等于圆周角的两倍)
∴∠TCB=∠CAB(定理:弦切角的度数等于它所夹的弧的圆周角)|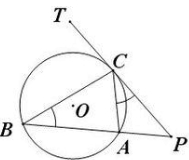
弦切角推论
若两弦切角所夹的弧相等,则这两个弦切角也相等.
弦切角定理的应用:
弦切角定理以及等弧对等角常用来证明角相等,由相似三角形常解决比例线段问题。
相交弦定理:
圆内的两条相交弦,被交点分成的两条线段长的积相等。
割线定理:
从圆外一点引圆的两条割线,这一点到每条割线与圆的交点的两条线段的长的积相等。
割线长定理:
从圆外一点引圆的切线和割线,切线长是这点到割线与圆交点的两条线段长的比例中项。
切线长定理:
从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线平分两条切线的夹角。
应用相交弦定理、切割线定理及推论的证明题的解决方法较多,常见的有:
(1)找过渡乘积式证明等积式成立;
(2)为三角形相似提供对应边成比例的条件;
(3)利用等积式来证明有关线段相等
相交弦定理、切割线定理及它们的推论和切线长定理的应用:
相交弦定理、切割线定理及它们的推论和切线长定理一样,揭示了和圆有关的一些线段间的数量关系,这些定理的证明及应用又常常和相似三角形联系在一起,因此在解题中要善于观察图形,对复杂的图形进行分解,找出基本图形和结论,从而准确地解决问题.另外在和圆有关的比例线段的计算问题中,要注意方程的思想的运用
与“(几何证明选讲)如图,点A、B、C都在⊙O上,过点C的切线交AB...”考查相似的试题有:
- 已知PA是圆O的切线,切点为A,PA=2,AC是圆O的直径,PC与圆O交于点B,PB=1,则圆O的半径R=( )。
- 如图,在梯形ABCD中,AB∥CD,AB=4,CD=2.E,F分别为AD,BC上点,且EF=3,EF∥AB,则梯形ABFE与梯形EFCD的面积比为______.
- 如图已知C点在圆O直径BE的延长线上,CA切⊙O于点,DC是∠ACB的平分线,交AE于点F,交AB于点D。(1)求∠ADF的度数;(2)若AB=AC...
- 设a>0,b>0,称2aba+b为a,b的调和平均数.如图,C为线段AB上的点,且AC=a,CB=b,O为AB中点,以AB为直径做半圆.过点C作AB...
- 如图⊙0的直径AD=2,四边形ABCD内接于⊙0,直线MN切⊙0于点B,∠MBA=30°,则AB的长为______.
- 如图,已知C点在圆O直径BE的延长线上,CA切圆O于A点,∠ACB的平分线分别交AE、AB于点F、D.(Ⅰ)求∠ADF的度数;(Ⅱ)若AB=AC...
- (选做题)已知PA是⊙O的切线,切点为A,直线PO交⊙O于B、C两点,AC=2,∠PAB=120°,则⊙O的面积为( ).
- 如图,已知⊙O的弦AB交半径OC于点D,若AD=3,BD=2,且D为OC的中点,则CD的长为______.
- 已知PA是圆O的切线,切点为A,PA=2,AC是圆O的直径,PC与圆O交于点B,PB=1,则AB=( )。
- (选做题)如图,△ABC是内接于⊙O,AB=AC,直线MN切⊙O于点C,弦BD∥MN,AC与BD相交于点E.(1)求证:△ABE≌△ACD;(2)若AB=6,...