本试题 “已知等差数列{an}的首项为a,公差为b,且不等式ax2-3x+2>0的解集为(-∞,1)∪(b,+∞),(1)求数列{an}的通项公式及前n项和Sn;(2)比较an和Sn-4的大小。” 主要考查您对等差数列的通项公式
等差数列的前n项和
比较法
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 等差数列的通项公式
- 等差数列的前n项和
- 比较法
等差数列的通项公式:
an=a1+(n-1)d,n∈N*。
an=dn+a1-d,d≠0时,是关于n的一次函数,斜率为公差d;
an=kn+b(k≠) {an}为等差数列,反之不能。
{an}为等差数列,反之不能。
对等差数列的通项公式的理解:
①从方程的观点来看,等差数列的通项公式中含有四个量,只要已知其中三个,即可求出另外一个.其中a1和d是基本量,只要知道a1和d即可求出等差数列的任一项;
②从函数的观点来看,在等差数列的通项公式中,。。是n的一次函数,其图象是直线y=dx+(a1-d)上均匀排开的一列孤立点,我们知道两点确定一条直线,因此,给出一个等差数列的任意两项,等差数列就被唯一确定了,
等差数列公式的推导:
等差数列的通项公式可由 归纳得出,当然,等差数列的通项公式也可用累加法得到:
归纳得出,当然,等差数列的通项公式也可用累加法得到:
等差数列的前n项和的公式:
(1)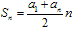 ,(2)
,(2)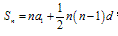 ,(3)
,(3)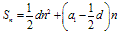 ,(4)
,(4)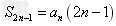
当d≠0时,Sn是关于n的二次函数且常数项为0,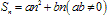
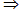 {an}为等差数列,反之不能。
{an}为等差数列,反之不能。
等差数列的前n项和的有关性质:
(1) ,…成等差数列;
,…成等差数列;
(2){an}有2k项时,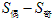 =kd;
=kd;
(3){an}有2k+1项时,S奇=(k+1)ak+1=(k+1)a平, S偶=kak+1=ka平,S奇:S偶=(k+1):k,S奇-S偶=ak+1=a平;
解决等差数列问题常用技巧:
1、等差数列中,已知5个元素:a1,an,n,d, S中的任意3个,便可求出其余2个,即知3求2。
为减少运算量,要注意设元的技巧,如奇数个成等差,可设为…,a-2d,a-d,a,a+d,a+2d,…,偶数个成等差,可设为…,a-3d,a-d,a+d,a+3d,…
2、等差数列{an}中,(1)若ap=q,aq=p,则列方程组可得:d=-1,a1=p+q-1,ap+q=0,S=-(p+q);
(2)当Sp=Sq时(p≠q),数形结合分析可得Sn中最大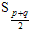 ,Sp+q=0,此时公差d<0。
,Sp+q=0,此时公差d<0。
比较法分类:
(1)求差比较法:要证a>b,只要证a-b>0;
(2)求商比较法:要证a>b,且b>0,只要证 >1;
>1;
比较法的步骤是:
作差(商)后通过分解因式、配方、通分等手段变形判断符号或与1的大小,然后作出结论。
实数比较大小的依据:
在数轴上不同的点A与点B分别表示两个不同的实数a与b,右边的点表示的数比左边的点表示的数大,从实数减法在数轴上的表示可以看出a、b之间具有以下性质:如图,如果a-b是正数,那么a>b;如果a-b是负数,那么a<b;如果a-b等于零,那么a=b,反之也成立,从而a-b>0等价于a>b;a-b=0等价于a=b;a-b<0等价于a<b.
比较数(式)的大小常用的方法:
(1)一是利用作差法来判断差的符号;二是利用作商法(分母为正时)来判断商与1的大小。这两种方法的关键是变形,常用的变形的技巧有因式分解、通分、配方、有理化等,当两个代数式正负不确定且为多项式形式时常用作差法比较大小.当两个代数式均为正且为幂的乘积式时常用作商法比较大小.
(2)比较大小时应熟记并应用“若a>b且ab>0则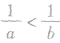 ”这一结论,不能强化也不能弱化条件,在此时应引起特别重视。
”这一结论,不能强化也不能弱化条件,在此时应引起特别重视。
与“已知等差数列{an}的首项为a,公差为b,且不等式ax2-3x+2>0的...”考查相似的试题有:
- 等比数列{an}中,已知a1=2,a4=16.(1)求数列{an}的通项公式;(2)若a3,a5分别为等差数列{bn}的第3项和第5项,试求数列{b...
- 已知等差数列{an}的公差d不为0,设Sn=a1+a2q+…+anqn-1,Tn=a1-a2q+…+(-1)n-1,q≠0,n∈N*.(1)若q=1,a1=1,S3=15,求数列...
- 已知等差数列{an}的前n项和为Sn,且a2=17,S10=100.(I)求数列{an}的通项公式;(II)若数列{bn}满足bn=ancos(nπ)+2n(n∈...
- 若等差数列{an}的前3项和S3=33,且a1=9,则a7=[ ]A.18B.19C.20D.21
- 设Sn是数列{an}的前n项和,且点(n,Sn)在函数y=x2+2x上,(1)求数列{an}的通项公式;(2)已知bn=2n-1,Tn=1a1.b1+1a2.b...
- 已知数列{an}为等差数列,且a1=-4,a3=4.(1)求数列{an}的通项公式;(2)求数列{an}的前n项和Sn.
- 数列{an}中,前n项和Sn=-n2-3,n∈N*,则{an}的通项公式为an=______.
- 等差数列{an}中,a1+a2+...+a9=81且a2+a3+...+a10=171,则公差d=( )
- 设Sn表示等差数列{an}的前n项和,且S9=18,Sn=240,若an-4=30(n>9),则n=______.
- 已知Sn是等差数列{an}的前n项和,且a1=1,a5=9,则S5=A.19B.25C.26D.30