本试题 “在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为矩形,AB=PA=BC(a>0),(Ⅰ)当a=1时,求证:BD⊥PC;(Ⅱ)若BC边上有且只有一个点Q,使得PQ⊥QD,求此时二面角A-PD-Q...” 主要考查您对直线与平面垂直的判定与性质
用向量方法解决线线、线面、面面的夹角问题
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 直线与平面垂直的判定与性质
- 用向量方法解决线线、线面、面面的夹角问题
线面垂直的定义:
如果一条直线l和一个平面α内的任何一条直线垂直,就说这条直线l和这个平面α互相垂直,记作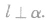 直线l叫做平面α的垂线,平面α叫做直线l的垂面。直线与平面垂直时,它们唯一的公共点P叫做垂足。
直线l叫做平面α的垂线,平面α叫做直线l的垂面。直线与平面垂直时,它们唯一的公共点P叫做垂足。
线面垂直的画法:
画线面垂直时,通常把直线画成与表示平面的平行四边形的一边垂直,如图所示:
线面垂直的判定定理:
如果一条直线和一个平面内的两条相交直线都垂直,那么这条直线垂直这个平面。(线线垂直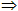 线面垂直)
线面垂直)
符号表示:
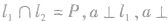
 如图所示,
如图所示,
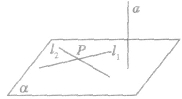
线面垂直的性质定理:
如果两条直线同垂直于一个平面,那么这两条直线平行。
(线面垂直 线线平行)
线线平行)
线面垂直的判定定理的理解:
(1)判定定理的条件中,“平面内的两条相交直线”是关键性语句,一定要记准.
(2)如果一条直线垂直于平面内的两条直线,那么这条直线垂直于这个平面,这个结论是错误的.
(3)如果一条直线垂直于平面内的无数条直线,那么这条直线垂直于这个平面,这个结论也错误,因为这无数条直线可能平行.
证明线面垂直的方法:
(1)线面垂直的定义拓展了线线垂直的范围,线垂直于面,线就垂直于面内所有直线,这也是线面垂直的必备条件,利用这个条件可将线线垂直与线面垂直互相转化,这样就完成了空间问题与平面问题的转化.
(2)证线面垂直的方法①利用定义:若一直线垂直于平面内任一直线,则这条直线垂直于该平面.②利用线面垂直的判定定理:证一直线与一平面内的两条相交直线都垂直,③利用线面垂直的性质:两平行线中的一条垂直于平面,则另一条也垂直于这个平面,④用面面垂直的性质定理:两平面垂直,在一个平面内垂直于交线的直线必垂直于另一个平面.⑤用面面平行的性质定理:一直线垂直于两平行平面中的一个,那么它必定垂直于另一个平面.⑥用面面垂直的性质:两相交平面同时垂直于第三个平面,那么两平面的交线垂直于第三个平面.⑦利用向量证明.
异面直线所成角:
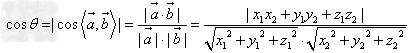 ,
,
(其中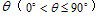 为异面直线a,b所成角,
为异面直线a,b所成角,![]() 分别表示异面直线a,b的方向向量)。
分别表示异面直线a,b的方向向量)。
直线AB与平面所成角:
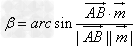 (
( 为平面α的法向量);
为平面α的法向量);
二面角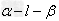 的平面角:
的平面角:
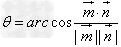 或
或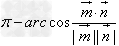 (
(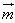 ,
, 为平面α,β的法向量)。
为平面α,β的法向量)。
用向量求异面直线所成角注意:
①求异面直线所成的角常用平移法或向量法,特别是向量法,由于降低了空间想象的要求,所以需引起我们的重视,用向量法时,需注意两异面直线夹角的范围是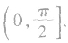
②两异面直线所成的角可以通过这两条直线的方向向量的夹角来求得,但二者不完全相等,当两方向向量的夹角是钝角时,应取其补角作为两异面直线所成的角.
求直线与平面所成的角既可选择传统立体几何的综合推理法,也可选择空间向量的向量法:
①求直线和平面所成角的步骤:作出斜线与其射影所成的角;证明所作的角就是要求的角;常在直角三角形(垂线、斜线、射影所组成的直角三角形)中解出所求角的大小:
②在用向量法求直线OP与α所成的角时一般有两种途径:一是直接求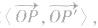 其中OP′,为斜线OP在平面α内的射影;二是通过求
其中OP′,为斜线OP在平面α内的射影;二是通过求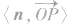 进而转化求解,其中n为平面α的法向量。
进而转化求解,其中n为平面α的法向量。
用向量求二面角注意:
①当法向量 的方向分别指向二面角的内侧与外侧时,二面角θ的大小等于法向量
的方向分别指向二面角的内侧与外侧时,二面角θ的大小等于法向量 的夹角
的夹角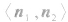 的大小;
的大小;
②当法向量 的方向同时指向二面角的内侧或外侧时,二面角θ的大小等于法向量
的方向同时指向二面角的内侧或外侧时,二面角θ的大小等于法向量 的夹角的补角
的夹角的补角 的大小.
的大小.
求二面角,大致有两种基本方法:
(1)传统立体几何的综合推理法:①定义法;②垂面法;③三垂线定理法;④射影面积法.
(2)空间向量的坐标法:建系并确定点及向量的坐标,分别求出两个平面的法向量,通过求两个法向量的夹角得出二面角的大小.
与“在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为矩形,AB=PA=BC(...”考查相似的试题有:
- 若将一个真命题中的“平面”换成“直线”、“直线”换成“平面”后仍是真命题,则该命题称为“可换命题”下列四个命题,其中是“可换命题...
- 如图,已知正三棱柱ABC-A1B1C1的底面边长为2,侧棱长为3,点E在侧棱AA1上,点F在侧棱BB1上,且AE=,BF=。(1)求证:CF⊥C1E;...
- 如图,多面体ABCDS中,面ABCD为矩形,SD⊥AD,且SD⊥AB,AD=1,AB=2,SD=,(1)求证:CD⊥平面ADS;(2)求AD与SB所成角的余弦...
- 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD为正方形,PA=AB=4,G为PD中点,E点在AB上,平面PEC⊥平面PDC,(Ⅰ)求证:A...
- 已知m,n是两条不同的直线,α,β是两个不同的平面,下列命题正确的是[ ]A、若m∥α,n∥α,则m∥nB、若α⊥β,m⊥β,mα,则m∥αC、若α...
- 设a、b为两条直线,α、β为两个平面,下列四个命题中,正确的命题是 ( )A、若a、b与α所成的角相等,则a∥bB、若a∥α,b∥β,α∥β,...
- 如图,四棱锥S﹣ABCD的底面为正方形,SD⊥底面ABCD,则下列结论中不正确的是[ ]A.AC⊥SB B.AB∥平面SCD C.SA与平面SBD所成的...
- 如图1,在直角梯形ABCD中,∠ADC=90°,CD∥AB,AB=4,AD=CD=2,M为线段AB的中点,将△ACD沿折起,使平面ACD⊥平面ABC,得到几何体...
- 已知平面α⊥平面β,α∩β=l,点A∈α,A,直线AB∥l,直线AC⊥l,直线m∥α,m∥β,则下列四种位置关系中,不一定成立的是[ ]A.AB∥mB.AC...
- 如图,四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD为梯形,AB∥DC,∠ABC=∠CAD=90°,且PA=AB=BC,点E是棱PB上的动点.(Ⅰ)当PD∥平...