返回

高中三年级数学

首页
首页 高中三年级数学知识 数列的极限 一般数列的项 反证法与放缩法 试题正文
  • 解答题

    已知不等式[log2n]，其中n为大于2的整数，[log2n]表示不超过log2n的最大整数。设数列{an}的各项为正，且满足a1=b（b＞0），an≤，n=2，3，4，…
    （Ⅰ）证明an＜，n=3，4，5，…
    （Ⅱ）猜测数列{an}是否有极限？如果有，写出极限的值（不必证明）；
    （Ⅲ）试确定一个正整数N，使得当n＞N时，对任意b＞0，都有an＜。


    本题信息：2012年模拟题数学解答题难度极难 来源:张玲玲
  • 本题答案
    查看答案
本试题 “已知不等式[log2n]，其中n为大于2的整数，[log2n]表示不超过log2n的最大整数。设数列{an}的各项为正，且满足a1=b（b＞0），an≤，n=2，3，4，…（Ⅰ）证明an＜，...” 主要考查您对

数列的极限

一般数列的项

反证法与放缩法

等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
  • 数列的极限
  • 一般数列的项
  • 反证法与放缩法

数列的极限定义（描述性的）：

如果当项数n无限增大时，无穷数列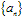的项an无限地趋近于某个常数a（即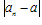无限地接近于0），a叫数列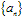的极限，记作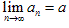，也可记做当n→+∞时，an→a。

数列的极限严格定义：

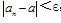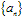即ε－N定义：对于任何正数ε（不论它多么小），总存在某正数N，使得当n＞N时，一切an都满足，a叫数列的极限。

数列极限的四则运算法则：

若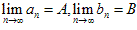，则
（1），；
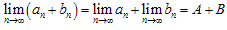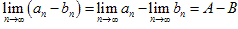（2），；
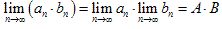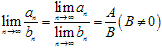（3）。
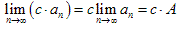前提条件：（1）各数列均有极限，（2）相加减时必须是有限个数列才能用法则。


an无限接近于a的方式有三种：

第一种是递增的数列，an无限接近于a，即an是在常数a的左边无限地趋近于a，如n→+∞时，；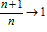
第二种是递减数列，an无限地趋近于a，即an是在常数a的右边无限地趋近于a，如n→+∞时，是；
第三种是摆动数列，an无限地趋近于a，即an是在无限摆动的过程中无限地趋近于a，如n→+∞时，。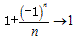


一些常用数列的极限：

（1）常数列A，A，A，…的极限是A；
（2）当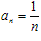时，；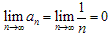
（3）当|q|＜1时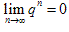，；当q＞1时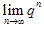，不存在；
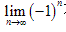（4）不存在，。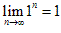
（5）无穷等比数列{an}中，首项a1，公比q，前n项和Sn，各项之和S，则（只有在0＜|q|＜1时）。


一般数列的项的定义：

数列中的每一个数叫做这个数列的项。


数列项的性质：

①数列的项具有有序性，一个数列不仅与构成数列的“数”有关，而且与这些数的排列顺序有关，注意与集合中元素的无序性区分开来，；
②数列的项具有可重复性，数列中的数可重复出现，这也要与集合中元素的互异性区分开来：
③注意an与{an}的区别：an表示数列{an}的第n 项，而{an}表示数列a1，a2，…，an，…，


方法提炼：

1.数列最大项、最小项、数列有界性问题可借助数列的单调性来解决，判断单调性时常用（1）作差法；（2）作差法；（3）结合函数图像等方法；
2.若求最大项an,则an满足an≥an+1且an≥an-1；若求最小项an,则an满足an≤an+1且an≤an-1。


反证法的定义：

有些不等式无法利用题设的已知条件直接证明，我们可以用间接的方法——反证法去证明，即通过否定原结论——导出矛盾——从而达到肯定原结论的目的。

放缩法的定义：

把原不等式放大或缩小成一个恰好可以化简的形式，比较常用的方法是把分母或分子适当放大或缩小（减去或加上一个正数）使不等式简化易证。


反证法证题的步骤：

若A成立，求证B成立。
共分三步：
（1）提出与结论相反的假设；如负数的反面是非负数，正数的反面是非正数即0和负数；
（2）从假设出发，经过推理，得出矛盾；（必须由假设出发进行推理否则不是反证法或证错）；
（3）由矛盾判定假设不正确，从而肯定命题的结论正确.矛盾：与定义、公理、定理、公式、性质等一切已有的结论矛盾甚至自相矛盾。
反证法是一种间接证明命题的基本方法。在证明一个数学命题时，如果运用直接证明法比较困难或难以证明时，可运用反证法进行证明。

放缩法的意义：

放缩法理论依据是不等式的传递性：若,a<b,b<c，则a<c.

放缩法的操作：

若求证P<Q，先证P<P1<P2<…<Pn,再证恰有Pn<Q.
需注意：（1）只有同方向才可以放缩，反方向不可。
（2）不能放（缩）得太大（小），否则不会有最后的Pn<Q.


发现相似题
与“已知不等式[log2n]，其中n为大于2的整数，[log2n]表示不超过l...”考查相似的试题有：