本试题 “已知函数f(x)=x2-|x|,则不等式f(log31x+1)<2的解为______.” 主要考查您对二次函数的性质及应用
对数函数的解析式及定义(定义域、值域)
对数函数的图象与性质
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 二次函数的性质及应用
- 对数函数的解析式及定义(定义域、值域)
- 对数函数的图象与性质
二次函数的定义:
一般地,如果 (a,b,c是常数,a≠0),那么y叫做x的二次函数。
(a,b,c是常数,a≠0),那么y叫做x的二次函数。
二次函数的图像:
是一条关于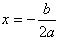 对称的曲线,这条曲线叫抛物线。
对称的曲线,这条曲线叫抛物线。
抛物线的主要特征:①有开口方向,a表示开口方向;a>0时,抛物线开口向上;a<0时,抛物线开口向下;
②有对称轴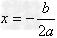 ;
;
③有顶点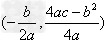 ;
;
④c表示抛物线与y轴的交点坐标:(0,c)。
性质:二次函数y=ax2+bx+c,
①当a>0时,函数f(x)的图象开口向上,在(-∞,-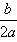 )上是减函数,在[-
)上是减函数,在[- ,+∞)上是增函数;
,+∞)上是增函数;
②当a<0时,函数f(x)的图象开口向下,在(-∞,-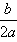 )上是增函数,在[-
)上是增函数,在[-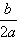 ,+∞)是减函数。
,+∞)是减函数。
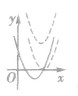
二次函数 (a,b,c是常数,a≠0)的图像:
(a,b,c是常数,a≠0)的图像:
| 图像 | 函数的性质 | ||
| a>0 | 定义域 | x∈R(个别题目有限制的,由解析式确定) | |
 |
值域 | a>0 | a<0 |
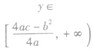 |
 | ||
| 奇偶性 | b=0时为偶函数,b≠0时为非奇非偶函数 | ||
| a<0 | 单调性 | a>0 | a<0 |
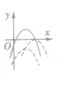 |
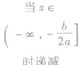 |
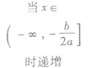 | |
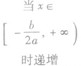 |
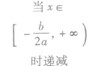 | ||
| 图像特点 |
 | ||
二次函数的解析式:
(1)一般式: (a,b,c是常数,a≠0);
(a,b,c是常数,a≠0);
(2)顶点式:若二次函数的顶点坐标为(h,k),则其解析式为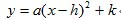 ;
;
(3)双根式:若相应一元二次方程的两个根为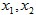 ,则其解析式为
,则其解析式为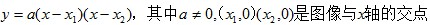 。
。
二次函数在闭区间上的最值的求法:
(1)二次函数![]() 在区间[p,g]上的最值问题
在区间[p,g]上的最值问题
一般情况下,需要分![]()
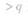 三种情况讨论解决.
三种情况讨论解决.
当a>0时,f(x)在区间[p,g]上的最大值为M,最小值为m,令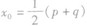 .
.
①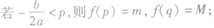
②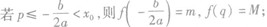
③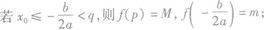
④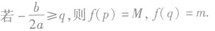
特别提醒:在区间内同时讨论最大值和最小值需要分四种情况讨论.
(2)二次函数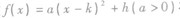 在区间[m.n]上的最值问题一般地,有以下结论:
在区间[m.n]上的最值问题一般地,有以下结论:
特别提醒:max{1,2}=2,即取集合{1,2}中最大的元素。
二次函数的应用:
(1)应用二次函数才解决实际问题的一般思路:
理解题意;建立数学模型;解决题目提出的问题。
(2)应用二次函数求实际问题中的最值:
即解二次函数最值应用题,设法把关于最值的实际问题转化为二次函数的最值问题,然后按求二次函数最值的方法求解。求最值时,要注意求得答案要符合实际问题。
对数函数的定义:
一般地,我们把函数y=logax(a>0,且a≠1)叫做对数函数,其中x是自变量,函数的定义域是(0,+∞),值域是R。
对数函数的解析式:
y=logax(a>0,且a≠1)
在解有关对数函数的解析式时注意:
在涉及到对数函数时,一定要注意定义域,即满足真数大于零;求值域时,还要考虑底数的取值范围。
对数函数的图形:
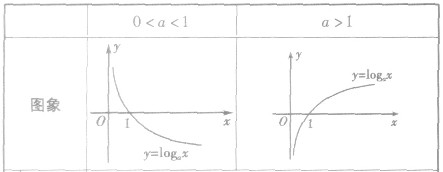
对数函数的图象与性质:
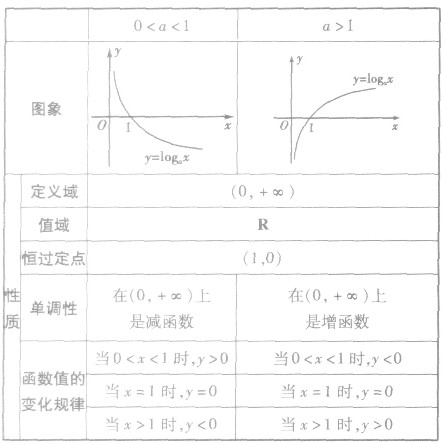
对数函数与指数函数的对比:
(1)对数函数与指数函数互为反函数,它们的定义域、值域互换,图象关于直线y=x对称.
(2)它们都是单调函数,都不具有奇偶性.当a>l时,它们是增函数;当O<a<l时,它们是减函数.
(3)指数函数与对数函数的联系与区别: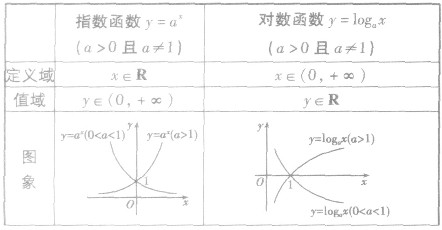
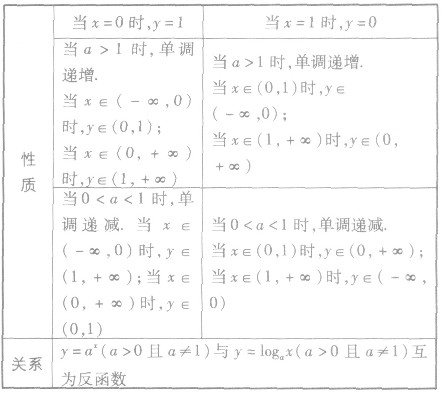
对数函数单调性的讨论:
解决与对数函数有关的函数单调性问题的关键:一是看底数是否大于l,当底数未明确给出时,则应对底数a是否大于1进行讨论;二是运用复合法来判断其单调性,但应注意中间变量的取值范围;三要注意其定义域(这是一个隐形陷阱),也就是要坚持“定义域优先”的原则.
利用对数函数的图象解题:
涉及对数型函数的图象时,一般从最基本的对数函数的图象人手,通过平移、伸缩、对称变换得到对数型函数的图象,特别地,要注意底数a>l与O<a<l的两种不同情况,
底数对函数值大小的影响:
1.在同一坐标系中分别作出函数
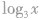 的图象,如图所示,可以看出:当a>l时,底数越大,图象越靠近x轴,同理,当O<a<l时,底数越小,函数图象越靠近x轴.利用这一规律,我们可以解决真数相同、对数不等时判断底数大小的问题.
的图象,如图所示,可以看出:当a>l时,底数越大,图象越靠近x轴,同理,当O<a<l时,底数越小,函数图象越靠近x轴.利用这一规律,我们可以解决真数相同、对数不等时判断底数大小的问题.
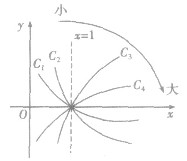
2.类似地,在同一坐标系中分别作出
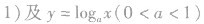 的图象,如图所示,它们的图象在第一象限的规律是:直线x=l把第一象限分成两个区域,每个区域里对数函数的底数都是由右向左逐渐减小,比如
的图象,如图所示,它们的图象在第一象限的规律是:直线x=l把第一象限分成两个区域,每个区域里对数函数的底数都是由右向左逐渐减小,比如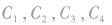 分别对应函数
分别对应函数
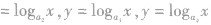 ,则必有
,则必有
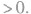
与“已知函数f(x)=x2-|x|,则不等式f(log31x+1)<2的解为______.”考查相似的试题有:
- 函数y=cos2x+5sinx-4的最大值为( ),最小值为( )。
- 设是某港口水的深度y(米)关于时间t(时)的函数,其中,下表是该港口某一天从0时至24时记录的时间t与水深y的关系t036912151...
- 若x∈(0,1),则下列关系式正确的是( )A.2x>lgxB.2x<lgxC.x12>2xD.lgx>x12
- 已知,试比较 与 的大小 ( ) A.B.C.D.无法比较大小
- 已知集合A={x|log2(2x)•log2x≤0}(1)求集合A;(2)求函数y=42x+1+4x,x∈A的值域.
- 设函数f(x)=若f(a)>f(-a),则实数a的取值范围是( )A.(-1,0)∪(0,1)B.(-∞,-1)∪(1,+∞)C.(-1,0)∪(1,+∞)D.(-∞,-1)∪(0,1)
- 函数f(x)=3x21-x+lg(2x+1)的定义域是______.
- 若函数y=f(x)是函数y=ax(a>0且a≠1)的反函数,且f(2)=1,则f(x)=[ ]A.log2xB.C.D.2x-2
- 已知,则[ ]A.a>b>cB.b>a>cC.a>c>bD.c>a>b
- 若log2x+log2y≥4,则x+y的最小值为( )A.8B.42C.2D.4