本试题 “直角坐标平面上三点A(1,2)、B(3,-2)、C(9,7),若E、F为线段BC的三等分点,则=( )。” 主要考查您对线段的定比分点
用坐标表示向量的数量积
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 线段的定比分点
- 用坐标表示向量的数量积
线段的定比分点定义:
设点P是直线P1P2上异于P1、P2的任意一点,若存在一个实数λ,使P1P=λPP2,λ叫做点P分有向线段 所成的比,P点叫做有向线段
所成的比,P点叫做有向线段  的以定比为λ的定比分点。
的以定比为λ的定比分点。
当P点在线段 P1P2上时,λ>0;当P点在线段 P1P2的延长线上时,λ<-1;当P点在线段P2P1的延长线上时 -1<λ<0。
若点P分有向线段 所成的比为λ,则点P分有向线段
所成的比为λ,则点P分有向线段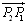 所成的比为
所成的比为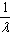 。
。
有向线段的定比分点的坐标公式:
(1)设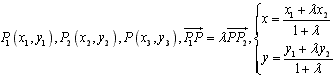 ,
,
在使用定比分点的坐标公式时,应明确(x,y),(x1,y1),(x2,y2)的意义,即分别为分点,起点,终点的坐标。一般在计算中应根据题设,自行确定起点,分点和终点并根据这些点确定对应的定比λ。
(2)当λ=1时,就得到P1P2的中点公式: ;
;
(3)三角形ABC的重心公式:设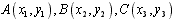 ,则重心
,则重心 。
。
两个向量的数量积的坐标运算:
非零向量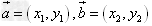 ,那么
,那么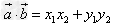 ,即两个向量的数量积等于它们对应坐标的乘积。
,即两个向量的数量积等于它们对应坐标的乘积。
向量的数量积的推广1:
设a=(x,y),则|a| =x2+y2 ,或|a|=
=x2+y2 ,或|a|=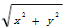
向量的数量积的推广2:
设 ,则
,则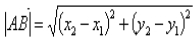
 ,则
,则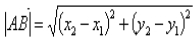
向量的数量积的坐标表示的证明:
已知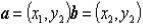 ,则
,则
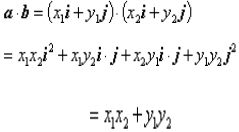
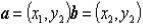 ,则
,则
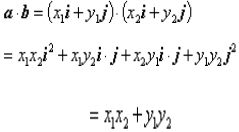
发现相似题
与“直角坐标平面上三点A(1,2)、B(3,-2)、C(9,7),若E、...”考查相似的试题有:
- a,b是不共线的两向量,其夹角是θ,若函数f(x)=(xa+b)•(a-xb)(x∈R)在(0,+∞)上有最大值,则( )A.|a|<|b|,且θ...
- 已知O为原点,点A,B的坐标分别是(a,0),(0,a),其中常数a>0,点P在线段AB上,且(0≤t≤1),则的最大值为A、a2B、aC、2aD...
- 在△ABC中,角A,B,C的对边分别为a,b,c,且满足(2a-c)cosB=bcosC。(1)求角B的大小。(2)设,当取最小值时,求的值。
- 已知向量=(sinA,cosA),=(,-1),,且A为锐角。(1)求角A的大小;(2)求函数f(x)=cos2x+4cosAsinx(x∈R)的值域。
- 直角坐标系xOy中,分别是与x轴,y轴平行的单位向量,若直角三角形ABC中,则k的可能值有( ) A.1个 B.2个 C.3个 D.4个
- 已知a=(2,4),b=(-1,-3),则|3a+2b|=______.
- 已知:点P是椭圆上的动点,F1、F2是该椭圆的左、右焦点。点Q满足与是方向相同的向量,又。(1)求点Q的轨迹C的方程;(2)是...
- 已知a=(1,0),b=(m,m)(m>0),则<a,b>=______.
- 已知a=(1,2),b=(3,-1),若存在向量c,使得a•c=3,b•c=9,则向量c的坐标为______.
- 在以O为原点的直角坐标系中,点A(4,-3)为△OAB的直角顶点,已知|AB|=2|OA|,且点B的纵坐标大于零。(1)求向量的坐标;(2...