本试题 “已知数列{an}的通项公式an=49-2n,则该数列的前n项和Sn取最大值时,n的取值为( )A.22B.23C.24D.25” 主要考查您对等差数列的通项公式
等差数列的前n项和
数列的概念及简单表示法
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 等差数列的通项公式
- 等差数列的前n项和
- 数列的概念及简单表示法
等差数列的通项公式:
an=a1+(n-1)d,n∈N*。
an=dn+a1-d,d≠0时,是关于n的一次函数,斜率为公差d;
an=kn+b(k≠) {an}为等差数列,反之不能。
{an}为等差数列,反之不能。
对等差数列的通项公式的理解:
①从方程的观点来看,等差数列的通项公式中含有四个量,只要已知其中三个,即可求出另外一个.其中a1和d是基本量,只要知道a1和d即可求出等差数列的任一项;
②从函数的观点来看,在等差数列的通项公式中,。。是n的一次函数,其图象是直线y=dx+(a1-d)上均匀排开的一列孤立点,我们知道两点确定一条直线,因此,给出一个等差数列的任意两项,等差数列就被唯一确定了,
等差数列公式的推导:
等差数列的通项公式可由 归纳得出,当然,等差数列的通项公式也可用累加法得到:
归纳得出,当然,等差数列的通项公式也可用累加法得到:
等差数列的前n项和的公式:
(1)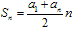 ,(2)
,(2)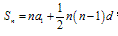 ,(3)
,(3)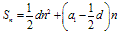 ,(4)
,(4)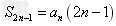
当d≠0时,Sn是关于n的二次函数且常数项为0,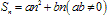
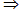 {an}为等差数列,反之不能。
{an}为等差数列,反之不能。
等差数列的前n项和的有关性质:
(1) ,…成等差数列;
,…成等差数列;
(2){an}有2k项时,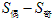 =kd;
=kd;
(3){an}有2k+1项时,S奇=(k+1)ak+1=(k+1)a平, S偶=kak+1=ka平,S奇:S偶=(k+1):k,S奇-S偶=ak+1=a平;
解决等差数列问题常用技巧:
1、等差数列中,已知5个元素:a1,an,n,d, S中的任意3个,便可求出其余2个,即知3求2。
为减少运算量,要注意设元的技巧,如奇数个成等差,可设为…,a-2d,a-d,a,a+d,a+2d,…,偶数个成等差,可设为…,a-3d,a-d,a+d,a+3d,…
2、等差数列{an}中,(1)若ap=q,aq=p,则列方程组可得:d=-1,a1=p+q-1,ap+q=0,S=-(p+q);
(2)当Sp=Sq时(p≠q),数形结合分析可得Sn中最大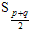 ,Sp+q=0,此时公差d<0。
,Sp+q=0,此时公差d<0。
数列的定义:
一般地按一定次序排列的一列数叫作数列,数列中的每一个数叫作这个数列的项,数列的一般形式可以写成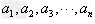 ,简记为数列{an},其中数列的第一项a1也称首项,an是数列的第n项,也叫数列的通项2、数列的递推公式:如果已知数列的第1项(或前几项),且从第2项(或某一项)开始的任一项an与它的前一项an-1(或前几项)间的关系可以用一个公式表示,那么这个公式就叫做这个数列的递推公式,递推公式也是给出数列的一种方法。
,简记为数列{an},其中数列的第一项a1也称首项,an是数列的第n项,也叫数列的通项2、数列的递推公式:如果已知数列的第1项(或前几项),且从第2项(或某一项)开始的任一项an与它的前一项an-1(或前几项)间的关系可以用一个公式表示,那么这个公式就叫做这个数列的递推公式,递推公式也是给出数列的一种方法。
从函数角度看数列:
数列可以看作是一个定义域为正整数集N'(或它的有限子集{l,2,3,…,n})的函数,即当自变量从小到大依次取值时对应的一列函数值,这里说的函数是一种特殊函数,其特殊性为自变量只能取正整数,且只能从I开始依次增大.可以将序号作为横坐标,相应的项作为纵坐标描点画图来表示一个数列,从数列的图象可以看出数列中各项的变化情况。
特别提醒:
①数列是一个特殊的函数,因此在解决数列问题时,要善于利用函数的知识、函数的观点、函数的思想方法来解题,即用共性来解决特殊问题;
②还要注意数列的特殊性(离散型),由于它的定义域是N'或它的子集{1,2,…,n},因而它的图象是一系列孤立的点,而不像我们前面所研究过的初等函数一般都是连续的曲线,因此在解决问题时,要充分利用这一特殊性.
与“已知数列{an}的通项公式an=49-2n,则该数列的前n项和Sn取最大...”考查相似的试题有:
- 等差数列{an}的前n项和是Sn,若a1+a2=5,a3+a4=9,则S10的值为( ) A.55 B.60 C.65 D.70
- 等比数列{an}和等差数列{bn}中,a5=b5,2a5-a2a8=0,则b3+b7=______.
- 已知等差数列{an}的公差为-2,且a1,a3,a4成等比数列.(Ⅰ)求数列{an}的通项公式;(Ⅱ)设{bn}是首项为1,公比2的等比数列...
- 数列1,11+2,11+2+3,11+2+3+4,…,11+2+…+n的前2009项的和( )A.20091005B.40142008C.20092008D.40162009
- 等差数列{an}的前项和为Sn,若a2+a8=12,则S9等于( )A.54B.45C.36D.27
- 在不超过2006的正整数中,能够被3整除的所有数之和为______.
- 已知等差数列an的前n项和为Sn,且a2+a4=-30,a1+a4+a7=-39,则使得Sn达到最小值的n是( )A.8B.9C.10D.11
- 已知等差数列{an}的前n项和Sn,其中a1+a5=12S5且a11=20,则S13=( )A.60B.130C.160D.260
- 一个机器人每一秒钟前进或后退一步,程序设计师让机器人以前进3步,然后再后退2步的规律移动.如果将机器人放在数轴的原点,...
- 数列{an}的通项公式an=cos7π2n,n∈N*,当n=______时,an有最小值.