本试题 “在直角坐标系xOy中,以坐标原点O为圆心的圆与直线:相切.(1)求圆O的方程;(2)若圆O上有两点M、N关于直线x+2y=0对称,且,求直线MN的方程;(3)圆O与x轴...” 主要考查您对向量数量积的运算
直线的方程
圆的标准方程与一般方程
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 向量数量积的运算
- 直线的方程
- 圆的标准方程与一般方程
两个向量数量积的含义:
如果两个非零向量 ,
, ,它们的夹角为
,它们的夹角为 ,我们把数量
,我们把数量 叫做
叫做 与
与 的数量积(或内积或点积),记作:
的数量积(或内积或点积),记作: ,即
,即 。
。 叫
叫 在
在 上的投影。
上的投影。
规定:零向量与任一向量的数量积是0,注意数量积是一个实数,不再是一个向量。
数量积的的运算律:
已知向量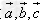 和实数λ,下面(1)(2)(3)分别叫做交换律,数乘结合律,分配律。
和实数λ,下面(1)(2)(3)分别叫做交换律,数乘结合律,分配律。
(1)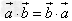 ;
;
(2)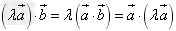 ;
;
(3)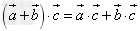 。
。
向量数量积的性质:
设两个非零向量
(1) ;
;
(2) ;
;
(3) ;
;
(4) ;
;
(5)当 ,
, 同向时,
同向时, ;当
;当 与
与 反向时,
反向时, ;当
;当 为锐角时,
为锐角时, 为正且
为正且 ,
, 不同向,
不同向, ;当
;当 为钝角时,
为钝角时, 为负且
为负且 ,
, 不反向,
不反向, 。
。
直线方程的定义:
以一个方程的解为坐标的点都是某条直线上的点,这个方程就叫做这条直线的方程,这条直线叫做这个方程的直线。
基本的思想和方法:
求直线方程是解析几何常见的问题之一,恰当选择方程的形式是每一步,然后釆用待定系数法确定方程,在求直线方程时,要注意斜率是否存在,利用截距式时,不能忽视截距为0的情形,同时要区分“截距”和“距离”。
直线方程的几种形式:
1.点斜式方程:
(1)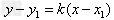 ,(直线l过点
,(直线l过点 ,且斜率为k)。
,且斜率为k)。
(2)当直线的斜率为0°时,k=0,直线的方程是y=y1。当直线的斜率为90°时,直线的斜率不存在,它的方程不能用点斜式表示,但因l上每一点的横坐标都等于x1,所以它的方程是x=x1。
2.斜截式方程:已知直线在y轴上的截距为b和斜率k,则直线的方程为:y=kx+b,它不包括垂直于x轴的直线。
3.两点式方程:已知直线经过(x1,y1),(x2,y2)两点,则直线方程为:
4.截距式方程:已知直线在x轴和y轴上的截距为a,b,则直线方程为: (a、b≠0)。
(a、b≠0)。
5.一般式方程:(1)定义:任何直线均可写成:Ax+By+C=0(A,B不同时为0)的形式。(2)特殊的方程如:平行于x轴的直线:y=b(b为常数);平行于y轴的直线:x=a(a为常数)。
几种特殊位置的直线方程:

(2)待定系数法:先设出直线的方程,再根据已知条件求出假设系数,最后代入直线方程,待定系数法常适用于斜截式,已知两点坐标等.
利用待定系数法求直线方程的步骤:①设方程;②求系数;③代入方程得直线方程,如果已知直线过一个定点
 ,可以利用直线的点斜式
,可以利用直线的点斜式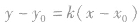 求方程,也可以利用斜截式、截距式等形式求解.
求方程,也可以利用斜截式、截距式等形式求解.圆的定义:
平面内与一定点的距离等于定长的点的集合是圆。定点就是圆心,定长就是半径。
圆的标准方程:
圆的标准方程 ,圆心(a,b),半径为r;特别当圆心是(0,0),半径为r时,圆的标准方程为
,圆心(a,b),半径为r;特别当圆心是(0,0),半径为r时,圆的标准方程为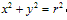 。
。
圆的一般方程:
圆的一般方程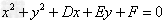
当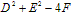 >0时,表示圆心在
>0时,表示圆心在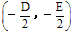 ,半径为
,半径为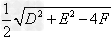 的圆;
的圆;
当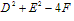 =0时,表示点
=0时,表示点 ;
;
当 <0时,不表示任何图形。
<0时,不表示任何图形。
圆的定义的理解:
(1)定位条件:圆心;定形条件:半径。
(2)当圆心位置与半径大小确定后,圆就唯一确定了.因此一个圆最基本的要素是圆心和半径.
圆的方程的理解:
(1)圆的标准方程中含有a,b,r三个独立的系数,因此,确定一个圆需三个独立的条件.其中圆心是圆的定位条件,半径是圆的定形条件.
(2)圆的标准方程的优点在于明确显示了圆心和半径.
(3)圆的一般方程形式的特点:
a.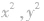 的系数相同且不等于零;
的系数相同且不等于零;
b.不含xy项.
(4)形如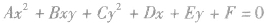 的方程表示圆的条件:
的方程表示圆的条件:
a.A=C≠0;
b.B=0;
c. 即
即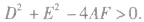
几种特殊位置的圆的方程:
| 条件 | 标准方程 | 一般方程 |
| 圆心在原点 |
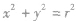 |
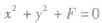 |
| 过原点 |
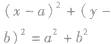 |
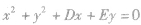 |
| 圆心在x轴上 |
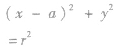 |
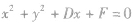 |
| 圆心在y轴上 |
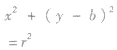 |
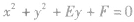 |
| 与x轴相切 |
 |
 |
| 与y轴相切 |
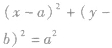 |
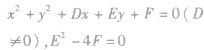 |
|
与x,y轴都相切 |
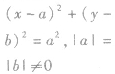 |
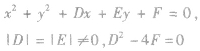 |
| 圆心在x轴上且过原点 |
 |
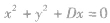 |
| 圆心在y轴上且过原点 |
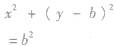 |
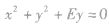 |
与“在直角坐标系xOy中,以坐标原点O为圆心的圆与直线:相切.(1...”考查相似的试题有:
- 已知m=(1,sinx),n=(cos(2x+π3),sinx),设函数f(x)=m•n.(1)求函数f(x)的最小正周期.(2)求函数f(x)的最大...
- 设a,b,c是向量,在下列命题中,正确的是______.①a•b=b•c,则a=c;②(a•b)•c=a•(b•c);③|a•b|=|a|•|b|④|a+b|2=(a+b)2...
- 下列说法正确的是( )A.经过定点P0(x0,y0)的直线都可以用方程y-y0=k(x-x0)表示B.经过定点A(0,b)的直线都可以用方...
- 已知两条直线l1:ax+8y+b=0和l2:2x+ay-1=0(b<0)若l1⊥l2且直线l1的纵截距为1时,a=______,b=______.
- 已知三角形ABC的顶点坐标为A(-1,5)、B(-2,-1)、C(4,3),M是BC边上的中点。(1)求AB边所在的直线方程;(2)求中线A...
- 如图所示,已知直线与轴的正半轴分别交于两点,直线和分别交于且平分△的面积,求的最小值.
- (本题8分)如图,已知点A(2,3), B(4,1),△ABC是以AB为底边的等腰三角形,点C在直线l:x-2y+2=0上.(Ⅰ)求AB边上的高CE所...
- 如果圆的方程为x2+y2+kx+2y+k2=0,那么当圆面积最大时,圆心坐标为( )A.(-1,1)B.(1,-1)C.(-1,0)D.(0,-1)
- (1)若AB=8,求直线的方程;(2)当直线的斜率为时,在上求一点P,使P到圆C的切线长等于PS;(3)设AB的中点为N,试在平面上...
- 圆x2+y2-4x-2y-5=0的圆心坐标是______.