本试题 “下列说法:①x>2是x2-3x+2>0的充分不必要条件.②函数y=x-1x+1图象的对称中心是(1,1).③已知x,y∈R,i为虚数单位,且(x-2)i-y=1+i,则(1+i)x-y的值为-...” 主要考查您对充分条件与必要条件
函数的单调性、最值
函数零点的判定定理
复数相等的充要条件
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 充分条件与必要条件
- 函数的单调性、最值
- 函数零点的判定定理
- 复数相等的充要条件
1、充分条件与必要条件:一般地,“若p,则q”为真命题,是指由p通过推理可以得出q,这时,我们就说,由p可推出q,记作 ,并且说p是q的充分条件,q是p的必要条件;
,并且说p是q的充分条件,q是p的必要条件;
2、充要条件:一般地,如果既有 ,又有
,又有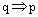 ,就记作
,就记作 ,此时,我们说,p是q的充分必要条件,简称充要条件。
,此时,我们说,p是q的充分必要条件,简称充要条件。
概括的说,如果 ,那么p与q互为充要条件。
,那么p与q互为充要条件。
3、充分不必要条件、必要不充分条件、既不充分也不必要条件:
①充分不必要条件:如果 ,且p
,且p q,则说p是q的充分不必要条件;
q,则说p是q的充分不必要条件;
②必要不充分条件:如果p q,且
q,且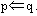 ,则说p是q的必要不充分条件;
,则说p是q的必要不充分条件;
③既不充分也不必要条件:如果p q,且p
q,且p q,则说p是q的既不充分也不必要条件。
q,则说p是q的既不充分也不必要条件。
单调性的定义:
1、对于给定区间D上的函数f(x),若对于任意x1,x2∈D,当x1<x2时,都有f(x1)<f(x2),则称f(x)是区间上的增函数;当x1<x2时,都有f(x1)>f(x2),则称f(x)是区间D上的减函数。
2、如果函数y=f(x)在区间上是增函数或减函数,就说函数y=f(x)在区间D上具有(严格的)单调性,区间D称为函数f(x)的单调区间。如果函数y=f(x)在区间D上是增函数或减函数,区间D称为函数f(x)的单调增或减区间
3、最值的定义:
最大值:一般地,设函数y=f(x)的定义域为I,如果存在实数M,满足: ①对于任意的x∈I,都有f(x)≤M;②存在x0∈I,使得f(x0)=M;那么,称M是f(x)的最大值.
最小值:一般地,设函数y=f(x)的定义域为I,如果存在实数M,满足: ①对于任意的x∈I,都有f(x)≥M;②存在x0∈I,使得f(x0)=M;那么,称M是f(x)的最小值
判断函数f(x)在区间D上的单调性的方法:
(1)定义法:其步骤是:
①任取x1,x2∈D,且x1<x2;
②作差f(x1)-f(x2)或作商 ,并变形;
,并变形;
③判定f(x1)-f(x2)的符号,或比较 与1的大小;
与1的大小;
④根据定义作出结论。
(2)复合法:利用基本函数的单调性的复合。
(3)图象法:即观察函数在区间D上部分的图象从左往右看是上升的还是下降的。
函数零点存在性定理:
一般地,如果函数y=f(x)在区间[a,b]上的图象是连续不断的一条曲线,并且有f(a).f(b)<o,那么函数y=f(x)在区间(a,b)内有零点,即存在c∈(a,b),使得f(c)=O,这个c也就是f(x)=0的根.特别提醒:(1)根据该定理,能确定f(x)在(a,b)内有零点,但零点不一定唯一.
(2)并不是所有的零点都可以用该定理来确定,也可以说不满足该定理的条件,并不能说明函数在(a,b)上没有零点,例如,函数f(x) =x2 -3x +2有f(0)·f(3)>0,但函数f(x)在区间(0,3)上有两个零点.
(3)若f(x)在[a,b]上的图象是连续不断的,且是单调函数,f(a).f(b)<0,则fx)在(a,b)上有唯一的零点.
函数零点个数的判断方法:
(1)几何法:对于不能用求根公式的方程,可以将它与函数y =f(x)的图象联系起来,并利用函数的性质找出零点.
特别提醒:①“方程的根”与“函数的零点”尽管有密切联系,但不能混为一谈,如方程x2-2x +1 =0在[0,2]上有两个等根,而函数f(x)=x2-2x +1在[0,2]上只有一个零点
②函数的零点是实数而不是数轴上的点.
(2)代数法:求方程f(x)=0的实数根.
两个复数相等的定义:
如果两个复数的实部和虚部分别相等,那么我们就说这两个复数相等,即:如果a,b,c,d∈R,那么a+bi=c+di a=c,b=d。特殊地,a,b∈R时,a+bi=0
a=c,b=d。特殊地,a,b∈R时,a+bi=0 a=0,b=0.
a=0,b=0.
复数相等的充要条件,提供了将复数问题化归为实数问题解决的途径。
复数相等特别提醒:
一般地,两个复数只能说相等或不相等,而不能比较大小。如果两个复数都是实数,就可以比较大小,也只有当两个复数全是实数时才能比较大小。
解复数相等问题的方法步骤:
(1)把给的复数化成复数的标准形式;
(2)根据复数相等的充要条件解之。
与“下列说法:①x>2是x2-3x+2>0的充分不必要条件.②函数y=x-1x+...”考查相似的试题有:
- 已知,都是实数,则“”是“”的( )A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分又不必要条件
- 已知条件甲:ab>0;条件乙:a>0,且b>0,则[ ]A.甲是乙的充分但不必要条件B.甲是乙的必要但不充分条件C.甲是乙的充要条件D...
- 若集合A={x|x2-5x+4
- “x<-1”是“x2-1>0”的[ ]A.充分而不必要条件B.必要而不充分条件C.充要条件D.既不充分也不必要条件
- 已知二次函数为偶函数,集合A=为单元素集合(I)求的解析式(II)设函数,若函数在上单调,求实数的取值范围.
- 已知函数f(x)=e|lnx|+a|x-1|(a为实数)(I)若a=1,判断函数f(x)在区间[1,+∞)上的单调性(不必证明);(II)若对于任...
- 定义区间(a,b),[a,b),(a,b],[a,b]的长度均为d=b-a,多个区间并集的长度为各区间长度之和,例如,(1,2)∪[3,5)...
- 设函数f(x)的定义域为D,若存在非零数l使得对于任意x∈M(MD)有x+l∈D,且f(x+l)≥f(x),则称f(x)为M上的l高调函数。现给出下列...
- 现向一个半径为R的球形容器内匀速注入某种液体,下面图形中能表示在注入过程中容器的液面高度h随时间t的函数关系的是( ) A...
- 函数f(x)=1x3-x的图象关于( )A.y轴对称B.直线y=-x对称C.坐标原点对称D.直线y=x对称