本试题 “已知数列{an}的前n项和为.(1)求数列{an}的通项公式;(2)若bn=log4an,求b1+b2+…+bn的值.” 主要考查您对对数与对数运算
等比数列的通项公式
数列求和的其他方法(倒序相加,错位相减,裂项相加等)
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 对数与对数运算
- 等比数列的通项公式
- 数列求和的其他方法(倒序相加,错位相减,裂项相加等)
对数的定义:
如果ax=N(a>0,且a≠1),那么数x叫做以a为底N的对数,记做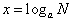 ,其中a叫做对数的底数,N叫做真数。
,其中a叫做对数的底数,N叫做真数。
通常以10为底的对数叫做常用对数,记做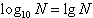 ;
;
以无理数e=2.71828…为底的对数叫做自然对数,记做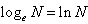 。
。
由定义知负数和0没有对数。
常用对数:
以10为底的对数叫做常用对数, 。
。
自然对数:
以e为底的对数叫做自然对数,e是无理数,e≈-2. 718 28, 。
。
对数的运算性质:
如果a>0,且a≠1,M>0,N>0,那么
(1)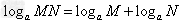 ;
;
(2)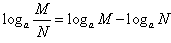 ;
;
(3) ;
;
(4) 。
。
对数的恒等式:
(1)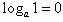 ;(2)
;(2)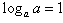 ;
;
(3)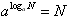 ;(4)
;(4) ;
;
(5)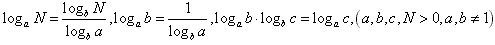 。
。
对数的换底公式及其推论:
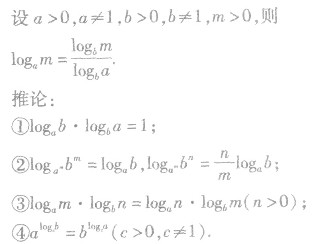
对数式的化简与求值:
(1)化同底是对数式变形的首选方向,其中经常用到换底公式及其推论.
(2)结合对数定义,适时进行对数式与指数式的互化.
(3)利用对数运算法则,在积、商、幂的对数与对数的和、差、倍之间进行转化,
等比数列的通项公式:
an=a1qn-1,q≠0,n∈N*。
等比数列的通项公式的理解:
①在已知a1和q的前提下,利用通项公式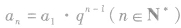 可求出等比数列中的任意一项;
可求出等比数列中的任意一项;
②在已知等比数列中任意两项的前提下,使用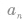
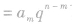 可求等比数列中任何一项;
可求等比数列中任何一项;
③用函数的观点看等比数列的通项,等比数列{an}的通项公式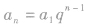 ,可以改写为
,可以改写为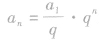 .当q>o,且q≠1时,y=qx是一个指数函数,而
.当q>o,且q≠1时,y=qx是一个指数函数,而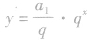 是一个不为0的常数与指数函数的积,因此等比数列{an}的图象是函数
是一个不为0的常数与指数函数的积,因此等比数列{an}的图象是函数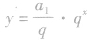 的图象上的一群孤立的点;
的图象上的一群孤立的点;
④通项公式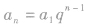 亦可用以下方法推导出来:
亦可用以下方法推导出来: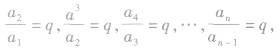
将以上(n一1)个等式相乘,便可得到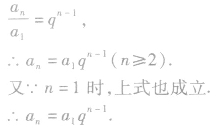
⑤用方程的观点看通项公式.在an,q,a1,n中,知三求一。
数列求和的常用方法:
1.裂项相加法:数列中的项形如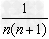 的形式,可以把
的形式,可以把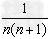 表示为
表示为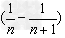 ,累加时抵消中间的许多项,从而求得数列的和;
,累加时抵消中间的许多项,从而求得数列的和;
2、错位相减法:源于等比数列前n项和公式的推导,对于形如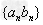 的数列,其中
的数列,其中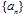 为等差数列,
为等差数列,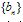 为等比数列,均可用此法;
为等比数列,均可用此法;
3、倒序相加法:此方法源于等差数列前n项和公式的推导,目的在于利用与首末两项等距离的两项相加有公因式可提取,以便化简后求和。
4、分组转化法:把数列的每一项分成两项,或把数列的项“集”在一块重新组合,或把整个数列分成两个部分,使其转化为等差或等比数列,这一求和方法称为分组转化法。
5、公式法求和:所给数列的通项是关于n的多项式,此时求和可采用公式求和,常用的公式有:
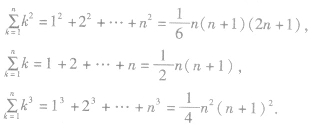
数列求和的方法多种多样,要视具体情形选用合适方法。
数列求和特别提醒:
(1)对通项公式含有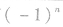 的一类数列,在求
的一类数列,在求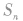 时,要注意讨论n的奇偶性;
时,要注意讨论n的奇偶性;
(2)在用等比数列前n项和公式时,一定要分q=1和q≠1两种情况来讨论。
与“已知数列{an}的前n项和为.(1)求数列{an}的通项公式;(2)...”考查相似的试题有:
- 已知lg2=a,lg3=b,用表示的值为 .
- 2log510+log50.25=[ ]A.0B.1C.2D.4
- 对于任意实数x, 符号[x]表示x的整数部分, 即[x]是“不超过x的最大整数”, 在数轴上, 当x是整数, [x]就是x,当x不是整数, [x]是点...
- 关于函数f(x)=lg(x>0,x∈R),下列命题正确的是________.(填序号)①函数y=f(x)的图象关于y轴对称;②在区间(-∞,0)上,函数y...
- 已知数列的前n项和为Sn,且满足.(1)求数列{an}的通项公式;(2)若bn=log2an,,且数列{cn}的前n项和为Tn,求Tn的取值范围.
- 已知数列{an}是等差数列,且a2=7,a5=16,数列{bn}是各项为正数的数列,且b1=2,点(log2bn,log2bn+1)在直线y=x+1上.(1)...
- 设函数.(1) 讨论函数f(x)的单调性;(2)若x≥0时,恒有f(x)≤ax3,试求实数a的取值范围;(3)令,试证明:.
- 已知数列{an}是等差数列,a2=6,a5=18;数列{bn}的前n项和是Tn,且。(1)求数列{an}的通项公式;(2)求证:数列{bn}是等比...
- 已知数列{an}的首项a1=1,a2=3,前n项的和为Sn,且Sn+1、Sn、Sn﹣1(n≥2)分别是直线l上的点A、B、C的横坐标,,设b1=1,bn+1...
- 设数列{an}的前n项和为Sn,已知a1=1,Sn=2n+1-n-2(n∈N*),(Ⅰ)求数列{an}的通项公式;(Ⅱ)若bn=nan+1-an,数列{bn}的前项...