本试题 “关于x,y的方程x2+y2=(xcosθ+ysinθ+2)2(0≤θ<2π)表示的曲线是( )(只需说明曲线类型);当θ变化时,该曲线的顶点的轨迹方程是( )。” 主要考查您对抛物线的标准方程及图象
抛物线的参数方程
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 抛物线的标准方程及图象
- 抛物线的参数方程
抛物线的标准方程及图像(见下表):

抛物线的标准方程的理解:
①抛物线的标准方程是指抛物线在标准状态下的方程,即顶点在原点,焦点在坐标轴上;
②抛物线的标准方程中的系数p叫做焦参数,它的几何意义是:焦点到准线的距离.焦点到顶点以及顶点到准线的距离均为
③抛物线的标准方程有四种类型,所以判断其类型是解题的关键,在方程的类型已确定的前提下,由于标准方程只有一个参数p,所以只需一个条件就可以确定一个抛物线的方程;
④对以上四种位置不同的抛物线和它们的标准方程进行对比、分析,得出其异同点。
共同点:
a.原点在抛物线上;
b.焦点都在坐标轴上;
c.准线与焦点所在轴垂直,垂足与焦点分别关于原点对称,它们与原点的距离都等于一次项系数的绝对值的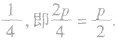
不同点:
a.焦点在x轴上时,方程的右侧为±2px,左端为y2;焦点在y轴上时,方程的右端为±2py,左端为x2;
b.开口方向与x轴(或y轴)的正半轴相同,焦点在x轴(或y轴)的正半轴上,方程右端取正号;开口方向与x轴(或y轴)的负半轴相同,焦点在x轴(或y轴)的负半轴上,方程的右端取负号.
求抛物线的标准方程的常用方法:
(1)定义法求抛物线的标准方程:定义法求曲线方程是经常用的一种方法,关键是理解定义的实质及注意条件,将所给条件转化为定义的条件,当然还应注意特殊情况.
(2)待定系数法求抛物线的标准方程:求抛物线标准方程常用的方法是待定系数法,为避免开口不确定,分成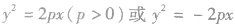 (p>0)两种情况求解的麻烦,可以设成
(p>0)两种情况求解的麻烦,可以设成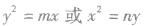 (m,n≠0),若m、n>0,开口向右或向上;m、n<0,开口向左或向下;m、n有两解,则抛物线的标准方程各有两个。
(m,n≠0),若m、n>0,开口向右或向上;m、n<0,开口向左或向下;m、n有两解,则抛物线的标准方程各有两个。
抛物线的参数方程:
如图,抛物线y2=2px(p>0)(或x2=2py(p>0))的参数方程为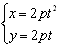 (或
(或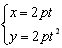 )(t为参数,t∈R)。
)(t为参数,t∈R)。
几何意义为:
t表示抛物线上除顶点外的任意一点与原点连线的斜率的倒数。即M(x,y)为抛物线上任意一点,则有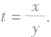
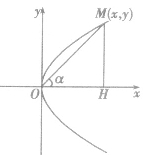
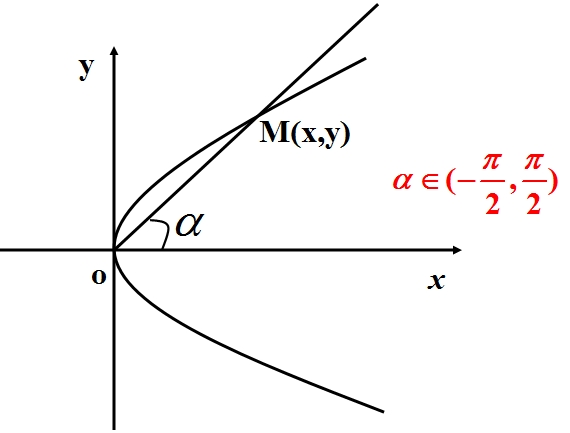
设抛物线的普通方程为
因为点M在α的终边上,根据三角函数的定义可得
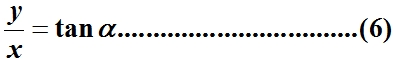
由(5)(6)解出x,y,得到
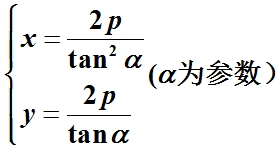
这就是抛物线(5)(不包括顶点)的参数方程。
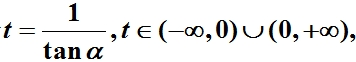 则有
则有
当t=0时,由参数方程表示的点正好就是抛物线的顶点(0,0),因此
与“关于x,y的方程x2+y2=(xcosθ+ysinθ+2)2(0≤θ<2π)表示的曲...”考查相似的试题有:
- 动点P在x轴与直线l:y=3之间的区域(含边界)上运动,且到点F(0,1)和直线l的距离之和为4,(Ⅰ)求点P的轨迹C的方程;(Ⅱ)过点Q(...
- 已知中心在原点,焦点在x轴上的椭圆,离心率e=22,且经过抛物线x2=4y的焦点.(1)求椭圆的标准方程;(2)若过点B(0,-2)...
- 平面直角坐标系中,O为坐标原点,已知两点M(1,-3)、N(5,1),若点C满足OC=tOM+(1-t)ON(t∈R),点C的轨迹与抛物线:y2...
- 已知平面内一动点到点F(1,0)的距离与点P到y轴的距离的等等于1。(1)求动点P的轨迹C的方程;(2)过点F作两条斜率存在且互...
- 已知直线l:y=12x-54,抛物线C:y2=2px(p>0)的顶点关于直线l的对称点在该抛物线上,求抛物线C的方程.
- 已知点M(1,y)在抛物线C:y2=2px(p>0)上,M点到抛物线C的焦点F的距离为2,直线l:y=-12x+b与抛物线交于A,B两点.(Ⅰ)...
- 设双曲线x2a2-y2b2=1(a>0,b>0)的离心率为54,抛物线y2=20x的准线过双曲线的左焦点,则此双曲线的方程为( )A.x24-y23=...
- 已知抛物线y2=-2px(p>0),过其焦点的直线与抛物线交于M(x1,y1),N(x2,y2),若x1x2=1,则抛物线准线方程为( ) x=B....
- 已知动点M到定点F(1,0)的距离与到定直线l:x=-1的距离相等,点C在直线上。(1)求动点M的轨迹方程;(2)设过定点F,法向...
- △AOB是边长为1的等边三角形,O是原点,AB⊥x轴,以O为顶点,且过A,B的抛物线的方程是( ) A.y2= B.y2=±x C.y2=-x D.y2=x