本试题 “已知下列命题四个命题:①若f(x)是定义在[-1,1]上的偶函数,且在[-1,0)上是增函数,θ∈(π4,π2),则f(sinθ)>f(cosθ);②在△ABC中,A>B是cosA<cosB的...” 主要考查您对真命题、假命题
充分条件与必要条件
余弦定理
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 真命题、假命题
- 充分条件与必要条件
- 余弦定理
命题的概念:
1、命题:把语言、符号或式子表达的,可以判断真假的陈述句称为命题;
2、真命题、假命题:判断为真的语句称为真命题,判断为假的语句称为假命题。
注意:
1、并不是所有的语句都是命题,只有能够判断真假的语句才是命题。
2、如果一个语句是命题,则它是真命题或是假命题,二者必具其一。
1、充分条件与必要条件:一般地,“若p,则q”为真命题,是指由p通过推理可以得出q,这时,我们就说,由p可推出q,记作 ,并且说p是q的充分条件,q是p的必要条件;
,并且说p是q的充分条件,q是p的必要条件;
2、充要条件:一般地,如果既有 ,又有
,又有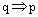 ,就记作
,就记作 ,此时,我们说,p是q的充分必要条件,简称充要条件。
,此时,我们说,p是q的充分必要条件,简称充要条件。
概括的说,如果 ,那么p与q互为充要条件。
,那么p与q互为充要条件。
3、充分不必要条件、必要不充分条件、既不充分也不必要条件:
①充分不必要条件:如果 ,且p
,且p q,则说p是q的充分不必要条件;
q,则说p是q的充分不必要条件;
②必要不充分条件:如果p q,且
q,且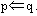 ,则说p是q的必要不充分条件;
,则说p是q的必要不充分条件;
③既不充分也不必要条件:如果p q,且p
q,且p q,则说p是q的既不充分也不必要条件。
q,则说p是q的既不充分也不必要条件。
余弦定理:
三角形任意一边的平方等于其他两边的平方的和减去这两边与它们夹角的余弦的积的两倍,
即 。
。
推论:
在△ABC中,若a2+b2=c2,则C为直角;若a2+b2>c2,则C为锐角;若a2+b2<c2,则C为钝角。
余弦定理在解三角形中的应用:
(1)已知两边和夹角,
(2)已知三边。
其它公式:
射影公式: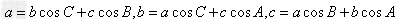
发现相似题
与“已知下列命题四个命题:①若f(x)是定义在[-1,1]上的偶函数...”考查相似的试题有:
- 有以下四个命题:①若x,y∈R,i为虚数单位,且(x-2)i-y=-1+i,则(1+i)x+y的值为-4;②将函数f(x)=cos(2x+π3)+1的图象向...
- 已知p:函数y=-(m-2)x为减函数;q:方程x2+ (m-2)x+1=0 无实根。若p∨q为真,p∧q为假,求m的取值范围。
- (本小题满分12分)已知p:≤2, q:>0)若非p是非q的必要不充分条件,求实数m的取值范围。
- 若,则是成立的( )A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件
- 设,则“xsin2x<1”是“xsinx<1”的[ ]A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件
- 给出下列四个命题:①在空间,若四点不共面,则每三个点一定不共线;②已知命题p、q,“非p为假命题”是“p或q是真命题”的必要不充...
- 已知函数,,则函数在上递增是在上递增的( )A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分又不必要条件
- 在△ABC中,角A,B,C所对的边分别为a,b,c,若sinA=3sinC,B=30°,b=2,则边c=______.
- 若△ABC的三边长为a,b,c,它的面积为a2+b2-c24,那么内角C等于( )A.30°B.45°C.60°D.90°
- (1)证明三角形的面积公式S=;(2)在△ABC中,求证:c(acosB-bcosA)=a2-b2。