本试题 “已知函数f(x)=∫x0t(t-4)dt;(1)若不等式f(x)+2x+2<m在[0,2]内有解,求实数m的取值范围;(2)若函数g(x)=f(x)+a-13在区间[0,5]上没有零点,求实数a的...” 主要考查您对二次函数的性质及应用
函数的最值与导数的关系
定积分的概念及几何意义
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 二次函数的性质及应用
- 函数的最值与导数的关系
- 定积分的概念及几何意义
二次函数的定义:
一般地,如果 (a,b,c是常数,a≠0),那么y叫做x的二次函数。
(a,b,c是常数,a≠0),那么y叫做x的二次函数。
二次函数的图像:
是一条关于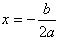 对称的曲线,这条曲线叫抛物线。
对称的曲线,这条曲线叫抛物线。
抛物线的主要特征:①有开口方向,a表示开口方向;a>0时,抛物线开口向上;a<0时,抛物线开口向下;
②有对称轴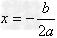 ;
;
③有顶点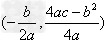 ;
;
④c表示抛物线与y轴的交点坐标:(0,c)。
性质:二次函数y=ax2+bx+c,
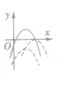
①当a>0时,函数f(x)的图象开口向上,在(-∞,-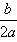 )上是减函数,在[-
)上是减函数,在[- ,+∞)上是增函数;
,+∞)上是增函数;
②当a<0时,函数f(x)的图象开口向下,在(-∞,-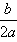 )上是增函数,在[-
)上是增函数,在[-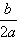 ,+∞)是减函数。
,+∞)是减函数。
二次函数 (a,b,c是常数,a≠0)的图像:
(a,b,c是常数,a≠0)的图像:
| 图像 | 函数的性质 | ||
| a>0 | 定义域 | x∈R(个别题目有限制的,由解析式确定) | |
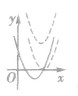 |
值域 | a>0 | a<0 |
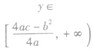 |
 | ||
| 奇偶性 | b=0时为偶函数,b≠0时为非奇非偶函数 | ||
| a<0 | 单调性 | a>0 | a<0 |
 |
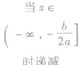 |
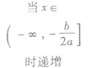 | |
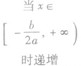 |
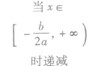 | ||
| 图像特点 |
 | ||
二次函数的解析式:
(1)一般式: (a,b,c是常数,a≠0);
(a,b,c是常数,a≠0);
(2)顶点式:若二次函数的顶点坐标为(h,k),则其解析式为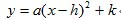 ;
;
(3)双根式:若相应一元二次方程的两个根为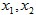 ,则其解析式为
,则其解析式为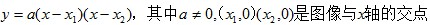 。
。
二次函数在闭区间上的最值的求法:
(1)二次函数![]() 在区间[p,g]上的最值问题
在区间[p,g]上的最值问题
一般情况下,需要分![]()
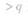 三种情况讨论解决.
三种情况讨论解决.
当a>0时,f(x)在区间[p,g]上的最大值为M,最小值为m,令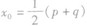 .
.
①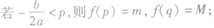
②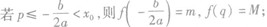
③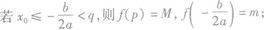
④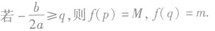
特别提醒:在区间内同时讨论最大值和最小值需要分四种情况讨论.
(2)二次函数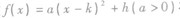 在区间[m.n]上的最值问题一般地,有以下结论:
在区间[m.n]上的最值问题一般地,有以下结论:
特别提醒:max{1,2}=2,即取集合{1,2}中最大的元素。
二次函数的应用:
(1)应用二次函数才解决实际问题的一般思路:
理解题意;建立数学模型;解决题目提出的问题。
(2)应用二次函数求实际问题中的最值:
即解二次函数最值应用题,设法把关于最值的实际问题转化为二次函数的最值问题,然后按求二次函数最值的方法求解。求最值时,要注意求得答案要符合实际问题。
函数的最大值和最小值:
在闭区间[a,b]上连续的函数f(x)在[a,b]上必有最大值与最小值,分别对应该区间上的函数值的最大值和最小值。
利用导数求函数的最值步骤:
(1)求f(x)在(a,b)内的极值;
(2)将f(x)的各极值与f(a)、f(b)比较得出函数f(x)在[a,b]上的最值。
用导数的方法求最值特别提醒:
①求函数的最大值和最小值需先确定函数的极大值和极小值,因此,函数极大值和极小值的判别是关键,极值与最值的关系:极大(小)值不一定是最大(小)值,最大(小)值也不一定是极大(小)值;
②如果仅仅是求最值,还可将上面的办法化简,因为函数fx在[a,b]内的全部极值,只能在f(x)的导数为零的点或导数不存在的点取得(下称这两种点为可疑点),所以只需要将这些可疑点求出来,然后算出f(x)在可疑点处的函数值,与区间端点处的函数值进行比较,就能求得最大值和最小值;
③当f(x)为连续函数且在[a,b]上单调时,其最大值、最小值在端点处取得。
生活中的优化问题:
生活中经常遇到求利润最大、用料最省、效率最高等问题,这些问题通常称为优化问题,解决优化问题的方法很多,如:判别式法,均值不等式法,线性规划及利用二次函数的性质等,
不少优化问题可以化为求函数最值问题.导数方法是解这类问题的有效工具.
用导数解决生活中的优化问题应当注意的问题:
(1)在求实际问题的最大(小)值时,一定要考虑实际问题的意义,不符合实际意义的值应舍去;
(2)在实际问题中,有时会遇到函数在区间内只有一个点使f'(x)=0的情形.如果函数在这点有极大(小)值,那么不与端点比较,也可以知道这就是最大(小)值;
(3)在解决实际优化问题时,不仅要注意将问题中涉及的变量关系用函数关系表示,还应确定出函数关系式中自变量的定义区间.
利用导数解决生活中的优化问题:
(1)运用导数解决实际问题,关键是要建立恰当的数学模型(函数关系、方程或不等式),运用导数的知识与方法去解决,主要是转化为求最值问题,最后反馈到实际问题之中.
(2)利用导数求f(x)在闭区间[a,b]上的最大值和最小值的步骤,
①求函数y =f(x)在(a,b)上的极值;
②将函数y=f(x)的各极值与端点处的函数值f(a)、f(b)比较,其中最大的一个是最大值,最小的一个是最小值.
(3)定义在开区间(a,b)上的可导函数,如果只有一个极值点,该极值点必为最值点.
定积分的定义:
设函数f(x)在[a,b]上有界(通常指有最大值和最小值),在a与b之间任意插入n-1个分点,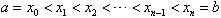 ,将区间[a,b]分成n个小区间
,将区间[a,b]分成n个小区间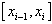 (i=1,2,…,n),记每个小区间的长度为
(i=1,2,…,n),记每个小区间的长度为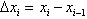 (i=1,2,…,n),在
(i=1,2,…,n),在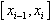 上任取一点ξi,作函数值f(ξi)与小区间长度
上任取一点ξi,作函数值f(ξi)与小区间长度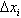 的乘积f(ξi)
的乘积f(ξi)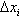 (i=1,2,…,n),并求和
(i=1,2,…,n),并求和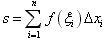 ,记λ=max{△xi;i=1,2,…,n },如果当λ→0时,和s总是趋向于一个定值,则该定值便称为函数f(x)在[a,b]上的定积分,记为
,记λ=max{△xi;i=1,2,…,n },如果当λ→0时,和s总是趋向于一个定值,则该定值便称为函数f(x)在[a,b]上的定积分,记为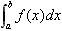 ,即
,即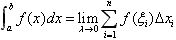 ,其中,
,其中, 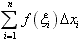 称为函数f(x)在区间[a,b]的积分和。
称为函数f(x)在区间[a,b]的积分和。
定积分的几何意义:
定积分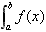 在几何上,
在几何上,
当f(x)≥0时,表示由曲线y=f(x)、直线x=a、直线x=b与x轴所围成的曲边梯形的面积;
当f(x)≤0时,表示由曲线y=f(x)、直线x=a、直线x=b与x轴所围成的曲边梯形的面积的负值;
一般情况下,表示介于曲线y=f(x)、两条直线x=a、x=b与x轴之间的个部分面积的代数和。
定积分的性质:
(1)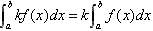 (k为常数);
(k为常数);
(2)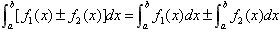 ;
;
(3)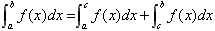 (其中a<c<b)。
(其中a<c<b)。
定积分特别提醒:
①定积分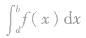 不是一个表达式,而是一个常数,它只与被积函数及积分区间有关,而与积分变量的记法无关,例如:
不是一个表达式,而是一个常数,它只与被积函数及积分区间有关,而与积分变量的记法无关,例如: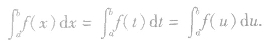
②定义中区间的分法和ξ的取法是任意的,
与“已知函数f(x)=∫x0t(t-4)dt;(1)若不等式f(x)+2x+2<m在[0...”考查相似的试题有:
- 函数y=x2+2(m+1)x+3在区间(-∞,2]上是减函数,则m的取值范围是[ ]A、m≤3B、m≥3C、m≤-3D、m≥-3
- 国家收购某种农产品价格为每吨120元,共中征税标准为每100元征收8元(称税率为8个百分点),计划可以收购a万吨,为减轻农民负...
- 已知b>-1,c>0,函数的图象与函数的图象相切.(Ⅰ)设(Ⅱ)是否存在常数c,使得函数内有极值点?若存在,求出c的取值范围;若...
- 函数的零点( )A.;B.;C.;D.。
- 已知为R上的可导函数,且满足,对任意正实数,下面不等式恒成立的是( )A.B.C.D.
- 某市旅游部门开发一种旅游纪念品,每件产品的成本是15元,销售价是20元,月平均销售2000件.通过改进工艺,产品的成本不变,...
- (13分)已知函数图象上一点P(2,)处的切线方程为(1)求的值(2)若方程在内有两个不等实根,求的取值范围(其中为自然对数...
- 若函数在上有最小值,实数的取值范围为________;
- 已知双曲线C:(a>b>0)和圆O:x2+y2=b2(其中原点O为圆心),过双曲线C上一点P(x0,y0)引圆O的两条切线,切点分别为A,B。...
- 已知函数则=( )A.1B.C.0D.