本试题 “已知数列{an}和{bn}满足a1=b1,且对任意n∈N*都有an+bn=1,,(Ⅰ)判断数列是否为等差数列,并说明理由;(Ⅱ)证明:。” 主要考查您对函数的单调性与导数的关系
等差数列的定义及性质
综合法与分析法证明不等式
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 函数的单调性与导数的关系
- 等差数列的定义及性质
- 综合法与分析法证明不等式
导数和函数的单调性的关系:
(1)若f′(x)>0在(a,b)上恒成立,则f(x)在(a,b)上是增函数,f′(x)>0的解集与定义域的交集的对应区间为增区间;
(2)若f′(x)<0在(a,b)上恒成立,则f(x)在(a,b)上是减函数,f′(x)<0的解集与定义域的交集的对应区间为减区间。
利用导数求解多项式函数单调性的一般步骤:
①确定f(x)的定义域;
②计算导数f′(x);
③求出f′(x)=0的根;
④用f′(x)=0的根将f(x)的定义域分成若干个区间,列表考察这若干个区间内f′(x)的符号,进而确定f(x)的单调区间:f′(x)>0,则f(x)在对应区间上是增函数,对应区间为增区间;f′(x)<0,则f(x)在对应区间上是减函数,对应区间为减区间。
函数的导数和函数的单调性关系特别提醒:
若在某区间上有有限个点使f′(x)=0,在其余的点恒有f′(x)>0,则f(x)仍为增函数(减函数的情形完全类似).即在区间内f′(x)>0是f(x)在此区间上为增函数的充分条件,而不是必要条件。
等差数列的定义:
一般地,如果一个数列从第2项起,每一项与它的前一项的差等于同一个常数,那么这个数列就叫做等差数列,这个常数叫做公差,用符号语言表示为an+1-an=d。
等差数列的性质:
(1)若公差d>0,则为递增等差数列;若公差d<0,则为递减等差数列;若公差d=0,则为常数列;
(2)有穷等差数列中,与首末两端“等距离”的两项和相等,并且等于首末两项之和;
(3)m,n∈N*,则am=an+(m-n)d;
(4)若s,t,p,q∈N*,且s+t=p+q,则as+at=ap+aq,其中as,at,ap,aq是数列中的项,特别地,当s+t=2p时,有as+at=2ap;
(5)若数列{an},{bn}均是等差数列,则数列{man+kbn}仍为等差数列,其中m,k均为常数。
(6)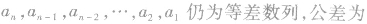
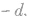
(7)从第二项开始起,每一项是与它相邻两项的等差中项,也是与它等距离的前后两项的等差中项,即

(8)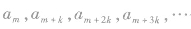 仍为等差数列,公差为
仍为等差数列,公差为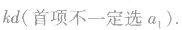
对等差数列定义的理解:
①如果一个数列不是从第2项起,而是从第3项或某一项起,每一项与它前一项的差是同一个常数,那么此数列不是等差数列,但可以说从第2项或某项开始是等差数列.
②求公差d时,因为d是这个数列的后一项与前一项的差,故有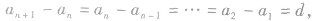 还有
还有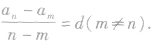
③公差d∈R,当d=0时,数列为常数列(也是等差数列);当d>0时,数列为递增数列;当d<0时,数列为递减数列;
④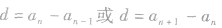 是证明或判断一个数列是否为等差数列的依据;
是证明或判断一个数列是否为等差数列的依据;
⑤证明一个数列是等差数列,只需证明an+1-an是一个与n无关的常数即可。
等差数列求解与证明的基本方法:
(1)学会运用函数与方程思想解题;
(2)抓住首项与公差是解决等差数列问题的关键;
(3)等差数列的通项公式、前n项和公式涉及五个量:a1,d,n,an,Sn,知道其中任意三个就可以列方程组求出另外两个(俗称“知三求二’).
综合法:
利用某些已知的不等式或已证过的不等式或不等式的性质推导出所要证的不等式成立,这种证明方法叫综合法,即由因导果。利用均值不等式的有关公式最为常见。
分析法:
(1)从求证的不等式出发,分析使这个不等式成立的充分条件,把证明这个不等式的问题转化为这些条件是否具备的问题,如果能肯定这些条件都已具备,那么就可以判定所证的不等式成立,这种证明方法叫分析法,即执果索因;
(2)用分析法证明要注意格式:“若A成立,则B成立”的模式是:欲证B为真,只需证C为真,只需证D为真…最后得出A或已知的性质、公理、定理,从而得出B为真。也可使用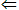 简化叙述。即B
简化叙述。即B C
C D
D …
… A或已知的性质、公理、定理。切不可使用B
A或已知的性质、公理、定理。切不可使用B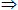 C
C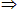 D
D …
…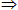 A。
A。
用综合法分析法证明不等式常用到的结论:

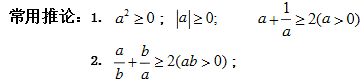
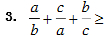 3,
3,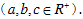
与“已知数列{an}和{bn}满足a1=b1,且对任意n∈N*都有an+bn=1,,...”考查相似的试题有:
- 设(其中),且当或时,方程只有一个实根;当时,方程有三个相异实根.现给出下列四个命题:①的任一实根大于的任一实根.②的...
- 设等差数列的前项和为且满足则中最大的项为( )A.B.C.D.
- 已知等差数列的公差为2,若成等比数列, 则= ( )A.–4B.–6C.–8D.–10
- 公差不为0的等差数列中,,数列是等比数列,且,则( )A.2B.4C.8D.16
- 若(x+12 4x)n展开式中前三项的系数成等差数列,求:(1)展开式中所有x的有理项;(2)展开式中系数最大的项.
- 已知正项等差数列的前n项和为,若,且,,成等比数列,(1)求数列的通项公式;(2)设,求数列的前n项和.
- 在各项均不为零的等差数列中,若,则( )A.B.C.D.
- 已知等差数列首项为,公差为,等比数列首项为,公比为,其中都是大于1的正整数,且,对于任意的,总存在,使得成立,则 ( )...
- 在等差数列{an}中,若a1+a2+a3+a4=30,则a2+a3=______.
- 已知数列{an}的通项公式为an=n2-n-30.(1)求数列的前三项,60是此数列的第几项?(2)n为何值时,an=0,an>0,an