本试题 “在△ABC中,角A、B、C的对边分别a、b、c,且2cos2A-B2cosB-sin(A-B)sinB+cos(A+C)=-35(1)求cosA的值;(2)若a=42,b=5,求向量BA在BC方向上的投影.” 主要考查您对两角和与差的三角函数及三角恒等变换
余弦定理
向量数乘运算及几何意义
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 两角和与差的三角函数及三角恒等变换
- 余弦定理
- 向量数乘运算及几何意义
两角和与差的公式:
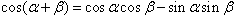
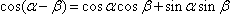
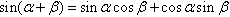
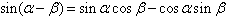
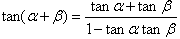
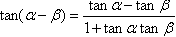
倍角公式:
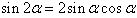
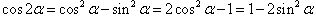
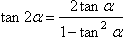
半角公式:
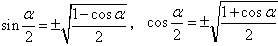
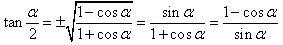
万能公式:
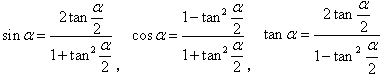
三角函数的积化和差与和差化积:
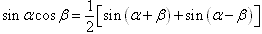

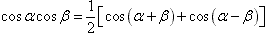
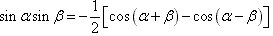
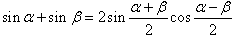
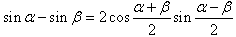
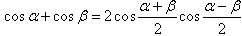
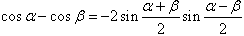
三角恒等变换:
寻找式子所包含的各个角之间的联系,并以此为依据选择可以联系它们的适当公式,这是三角恒等变换的特点。
三角函数式化简要遵循的"三看"原则:
(1)一看"角".这是最重要的一点,通过角之间的关系,把角进行合理拆分与拼凑,从而正确使用公式.
(2)二看"函数名称".看函数名称之间的差异,从而确定使用的公式.
(3)三看"结构特征".分析结构特征,可以帮助我们找到变形得方向,常见的有"遇到分式要通分"等.
方法提炼:
(1)解决给值求值问题的一般思路:
①先化简需求值得式子;②观察已知条件与所求值的式子之间的联系(从三角函数名及角入手);③将已知条件代入所求式子,化简求值.
(2)解决给值求角问题的一般步骤:
①求出角的某一个三角函数值;②确定角的范围;③根据角的范围确定所求的角.
余弦定理:
三角形任意一边的平方等于其他两边的平方的和减去这两边与它们夹角的余弦的积的两倍,
即 。
。
推论:
在△ABC中,若a2+b2=c2,则C为直角;若a2+b2>c2,则C为锐角;若a2+b2<c2,则C为钝角。
余弦定理在解三角形中的应用:
(1)已知两边和夹角,
(2)已知三边。
其它公式:
射影公式: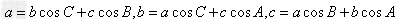
向量的数乘的定义:
我们规定实数λ与向量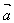 的积是一个向量,记作λ
的积是一个向量,记作λ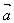 ;
;
向量的数乘的长度和方向规定如下:
(1)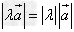 ;
;
(2)当λ>0时,λ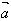 的方向与
的方向与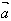 的方向相同;当λ<0时,λ
的方向相同;当λ<0时,λ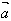 的方向与
的方向与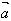 的方向相反;当λ=0时,
的方向相反;当λ=0时,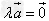 ;注意:λ
;注意:λ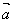 ≠0
≠0
数乘运算的坐标表示:
设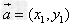 ,则
,则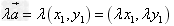 。
。
实数与向量积的运算律:
(1)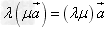 ;
;
(2)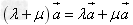 ;
;
(3)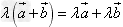 。
。
向量数乘运算的理解:
①向量数乘运算结果仍然是向量.
②实数与向量的积的特殊情况: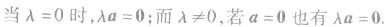
③实数与向量可以求积,但是不能进行加减运算,比如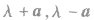 无意义。
无意义。
④由向量数乘的概念可知其几何意义,可以把向量a的长度扩大(当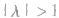 时),也可以缩小(当
时),也可以缩小(当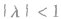 时),同时,我们可以不改变向量a的方向
时),同时,我们可以不改变向量a的方向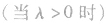 ,也可以改变向量a的方向(当λ<0时)。
,也可以改变向量a的方向(当λ<0时)。
与“在△ABC中,角A、B、C的对边分别a、b、c,且2cos2A-B2cosB-sin...”考查相似的试题有:
- 在△ABC中,角A、B、C的对边分别为a、b、c,且sinCcosB+sinBcosC=3sinAcosB.(1)求cosB的值;(2)若BA•BC=2,且b=22,求a和...
- 设函数的最小正周期为。(Ⅰ)求的值;(Ⅱ)若函数的图象是由的图象向右平移个单位长度得到,求的单调增区间。
- 看下图回答问题
- 在△ABC中,角A,B,C所对应的边分别为a,b,c,A,B为锐角且B<A,sinA=55,sin2B=35.(Ⅰ)求角C的值;(Ⅱ)若b+c=5+1,求a...
- 已知tanα=-13,cosβ=55,α,β∈(0,π)(1)求sinβ的值; (2)求tan(α+β)的值.
- .在中,角的对边分别为,则且,则等于( )A.B.C.4D.
- 已知在中,,则锐角的大小为( )
- 在△ABC中,角A、B、C的对边分别为a、b、c,且a2+ab=c2-b2,则角C等于[ ]A、B、C、D、
- 已知△ABC的三个内角A、B、C所对的三边分别是a、b、c,平面向量=(1,sin(B-A)),平面向量=(sinC-sin2A,1),(Ⅰ)如果c=2...
- 已知,若,则k=" "