本试题 “已知△ABC的三个内角A、B、C所对的三边分别是a、b、c,平面向量=(1,sin(B-A)),平面向量=(sinC-sin2A,1),(Ⅰ)如果c=2,C=,且△ABC的面积S=,求a的值;...” 主要考查您对正弦定理
面积定理:S=1/2absinC=1/2acsinB=1/2bcsinA
余弦定理
用坐标表示向量的数量积
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 正弦定理
- 面积定理:S=1/2absinC=1/2acsinB=1/2bcsinA
- 余弦定理
- 用坐标表示向量的数量积
正弦定理:
在一个三角形中,各边和它所对角的正弦的比相等,即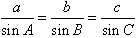 =2R。
=2R。
有以下一些变式:
(1)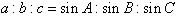 ;
;
(2)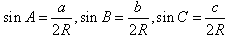 ;
;
(3)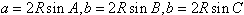 。
。
正弦定理在解三角形中的应用:
(1)已知两角和一边解三角形,只有一解。
(2)已知两边和其中一边的对角,解三角形,要注意对解的个数的讨论。可按如下步骤和方法进行:先看已知角的性质和已知两边的大小关系。
如已知a,b,A,
(一)若A为钝角或直角,当b≥a时,则无解;当a≥b时,有只有一个解;
(二)若A为锐角,结合下图理解。
①若a≥b或a=bsinA,则只有一个解。
②若bsinA<a<b,则有两解。
③若a<bsinA,则无解。 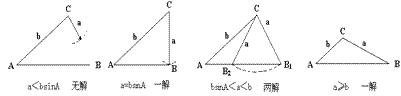
也可根据a,b的关系及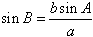 与1的大小关系来确定。
与1的大小关系来确定。
三角形面积公式:
(1)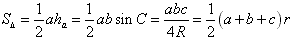
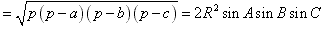 ,
,
其中r为三角形ABC内切圆半径,R为外接圆的半径, 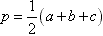 。
。
(2)数量积形式的三角形面积公式:
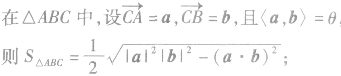
(3)坐标形式的三角形面积公式:

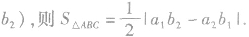
方法提炼:
(1)三角形的面积经常与正余弦定理结合在一起考查,解题时要注意方程思想的运用,即通过正余弦定理建立起方程(组),进而求得边或角;
(2)要熟记常用的面积公式及其变形.
余弦定理:
三角形任意一边的平方等于其他两边的平方的和减去这两边与它们夹角的余弦的积的两倍,
即 。
。
推论:
在△ABC中,若a2+b2=c2,则C为直角;若a2+b2>c2,则C为锐角;若a2+b2<c2,则C为钝角。
余弦定理在解三角形中的应用:
(1)已知两边和夹角,
(2)已知三边。
其它公式:
射影公式: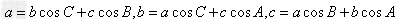
两个向量的数量积的坐标运算:
非零向量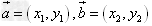 ,那么
,那么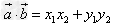 ,即两个向量的数量积等于它们对应坐标的乘积。
,即两个向量的数量积等于它们对应坐标的乘积。
向量的数量积的推广1:
设a=(x,y),则|a| =x2+y2 ,或|a|=
=x2+y2 ,或|a|=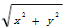
向量的数量积的推广2:
设 ,则
,则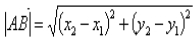
 ,则
,则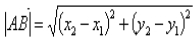
向量的数量积的坐标表示的证明:
已知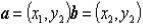 ,则
,则
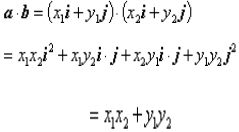
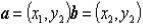 ,则
,则
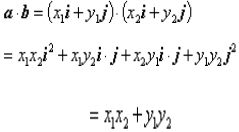
发现相似题
与“已知△ABC的三个内角A、B、C所对的三边分别是a、b、c,平面向...”考查相似的试题有:
- 在△ABC中,a、b、c分别是∠A、∠B、∠C所对边的边长,若(a+b+c)(sin A+sin B-sin C)=a·sin B,则∠C等于[ ]A.B.C.πD.π
- 在中,分别是三内角的对边,且,则角等于( )A.B.C.D.
- 在△ABC中.若b=5,∠B=π4,tanA=2,则sinA=______;a=______.
- △ABC中,∠A=π3,a=22,b=4,那么满足条件的△ABC( )A.有一个解B.有两个解C.无解D.不能确定
- 在△ABC中,AC=7,BC=2,cosB=12(Ⅰ)求sinA;(Ⅱ)求AB及△ABC的面积.
- 在海岸不远处有两个小岛P,Q,现要测量它们之间的距离,在岸边取两个点A、B,测得AB=50m,∠PAB=105°,∠QAB=30°,∠PBA=45°,∠Q...
- 在△ABC中,角A,B,C的对边分别为a,b,c.已知向量m=(2cosA2, sinA2),n=(cosA2, -2sinA2),m•n=-1,(Ⅰ) 求cosA的值;(...
- 在△ABC中,a2+b2=c2-ab,则角C=______°.
- 在△ABC中,A=120°,AB=5,BC=7,则的值为[ ]A、B、C、D、
- 某货轮在A处看灯塔B在货轮的北偏东75°的方向上,距离为126海里,在A处看灯塔C在货轮的北偏西30°的方向上,距离为83海里,货轮...