本试题 “如图所示,直三棱柱ABC-A1B1C1中,CA=CB=2,∠BCA=90°,棱AA1=4,E、M、N分别是CC1、A1B1、AA1的中点,(1)求证:A1B⊥C1M;(2)求BN的长;(3)求二面角B1-A...” 主要考查您对空间两点间的距离
用向量证明线线、线面、面面的垂直、平行关系
用向量方法解决线线、线面、面面的夹角问题
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 空间两点间的距离
- 用向量证明线线、线面、面面的垂直、平行关系
- 用向量方法解决线线、线面、面面的夹角问题
空间中两点的距离公式:
在空间直角坐标系中,设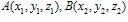 ,则AB两点间的距离
,则AB两点间的距离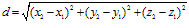 。
。
距离公式的理解:
(1)两点间的距离公式其形式与平面向量的长度公式一致,它的几何意义是表示长方体的对角线的长度.(2)两点间的距离公式与坐标原点的选取无关,dAB表示的是A,B两点间的距离,经过适当转化也可以求异面直线间的距离,点到面以及平面与平面的距离等.
中点坐标公式:



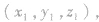

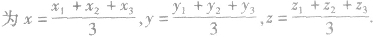
用向量证明线线、线面、面面的垂直、平行关系:
设直线l,m的方向向量为a,b,平面α,β的法向量为u,v,则
(1)线线平行l∥m  a∥b
a∥b  a=kb;
a=kb;
(2)线面平行l∥α  a⊥u
a⊥u  a·u=0;
a·u=0;
(3)线面垂直l⊥α a∥u
a∥u  a=ku;
a=ku;
(4)面面平行α∥β  u∥v
u∥v u=kv;
u=kv;
(5)面面垂直α⊥β u⊥v
u⊥v u·v=0。
u·v=0。
证明平行的其他方法:
①根据线面平行的判定定理:(平面外)与平面内的一条直线平行,那么这条直线和这个平面平行”,要证明一条直线和一个平面平行,也可以在平面内找一个向量与已知直线的方向向量是共线向量;
②根据共面向量定理可知,如果一个向量和两个不共线的向量是共面向量,那么这个向量与这两个不共线向量确定的平面必定平行,因此要证明一条直线和一个平面平行,只要证明这条直线的方向向量能够用平面内两个不共线向量线性表示即可.
异面直线所成角:
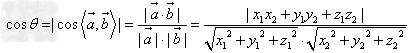 ,
,
(其中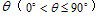 为异面直线a,b所成角,
为异面直线a,b所成角,![]() 分别表示异面直线a,b的方向向量)。
分别表示异面直线a,b的方向向量)。
直线AB与平面所成角:
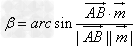 (
( 为平面α的法向量);
为平面α的法向量);
二面角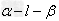 的平面角:
的平面角:
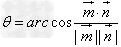 或
或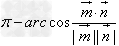 (
(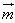 ,
, 为平面α,β的法向量)。
为平面α,β的法向量)。
用向量求异面直线所成角注意:
①求异面直线所成的角常用平移法或向量法,特别是向量法,由于降低了空间想象的要求,所以需引起我们的重视,用向量法时,需注意两异面直线夹角的范围是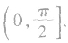
②两异面直线所成的角可以通过这两条直线的方向向量的夹角来求得,但二者不完全相等,当两方向向量的夹角是钝角时,应取其补角作为两异面直线所成的角.
求直线与平面所成的角既可选择传统立体几何的综合推理法,也可选择空间向量的向量法:
①求直线和平面所成角的步骤:作出斜线与其射影所成的角;证明所作的角就是要求的角;常在直角三角形(垂线、斜线、射影所组成的直角三角形)中解出所求角的大小:
②在用向量法求直线OP与α所成的角时一般有两种途径:一是直接求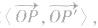 其中OP′,为斜线OP在平面α内的射影;二是通过求
其中OP′,为斜线OP在平面α内的射影;二是通过求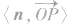 进而转化求解,其中n为平面α的法向量。
进而转化求解,其中n为平面α的法向量。
用向量求二面角注意:
①当法向量 的方向分别指向二面角的内侧与外侧时,二面角θ的大小等于法向量
的方向分别指向二面角的内侧与外侧时,二面角θ的大小等于法向量 的夹角
的夹角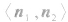 的大小;
的大小;
②当法向量 的方向同时指向二面角的内侧或外侧时,二面角θ的大小等于法向量
的方向同时指向二面角的内侧或外侧时,二面角θ的大小等于法向量 的夹角的补角
的夹角的补角 的大小.
的大小.
求二面角,大致有两种基本方法:
(1)传统立体几何的综合推理法:①定义法;②垂面法;③三垂线定理法;④射影面积法.
(2)空间向量的坐标法:建系并确定点及向量的坐标,分别求出两个平面的法向量,通过求两个法向量的夹角得出二面角的大小.
与“如图所示,直三棱柱ABC-A1B1C1中,CA=CB=2,∠BCA=90°,棱AA1=...”考查相似的试题有:
- 已知矩形中,,将沿着折成的二面角,则 两点的距离为
- 动点P在直线x+y=4上,O为原点,则|OP|的最小值为( )A.B.C.2D.2
- 直四棱柱的底面是菱形,,其侧面展开图是边长为的正方形.、分别是侧棱、上的动点,.(Ⅰ)证明:;(Ⅱ)在棱上,且,若∥平面,求.
- 已知直线和平面,且,那么( )A.B.不在内C.D.
- ( 12分)如图,在四棱锥中,侧面是正三角形,底面是边长为2的正方形,侧面平面为的中点.①求证:平面;②求直线与平面所成角的正切值.
- 如图,四棱锥的底面是平行四边形,,,面,设为中点,点在线段上且.(1)求证:平面;(2)设二面角的大小为,若,求的长.
- 如图,在直三棱柱ABC-A1B1C1中,AC=3,BC=4,AB=5,AA1=4,点D是AB的中点.(1)求证:∥平面;(2)求证:AC⊥BC1.
- 在如图所示的几何体中,四边形为平行四边形,,平面,,,,,且是的中点.(Ⅰ)求证:平面;(Ⅱ)求二面角的大小;(Ⅲ)在线...
- 如图,已知四棱锥P-ABCD的底面是正方形,PA⊥面ABCD,且PA=AD=2,点M,N分别在PD,PC上,,PM=MD,(Ⅰ)求证:PC⊥面AMN;(Ⅱ)...
- 在图(1)所示的长方形ABCD中,AD=2AB=2,E、F分别为AD、BC的中点,M、N两点分别在AF和CE上运动,且AM=EN=a(0<a<2).把长方...