返回

高中三年级数学

首页
首页 高中三年级数学知识 等差数列的定义及性质 一般数列的通项公式 递增数列和递减数列 试题正文
  • 解答题
    已知数列{an}，{bn}满足bn=an+1-an，其中n=1，2，3，…
    （Ⅰ）若a1=1，bn=n，求数列{an}的通项公式；
    （Ⅱ）若bn+1bn-1=bn（n≥2），且b1=1，b2=2，
    （ⅰ）记cn=a6n-1（n≥1），求证：数列{cn}为等差数列；
    （ⅱ）若数列中任意一项的值均未在该数列中重复出现无数次，求首项a1应满足的条件。
    本题信息：2011年北京期末题数学解答题难度极难 来源:张玲玲
  • 本题答案
    查看答案
本试题 “已知数列{an}，{bn}满足bn=an+1-an，其中n=1，2，3，…（Ⅰ）若a1=1，bn=n，求数列{an}的通项公式；（Ⅱ）若bn+1bn-1=bn（n≥2），且b1=1，b2=2，（ⅰ）记cn=a6n-1...” 主要考查您对

等差数列的定义及性质

一般数列的通项公式

递增数列和递减数列

等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
  • 等差数列的定义及性质
  • 一般数列的通项公式
  • 递增数列和递减数列

等差数列的定义：

一般地，如果一个数列从第2项起，每一项与它的前一项的差等于同一个常数，那么这个数列就叫做等差数列，这个常数叫做公差，用符号语言表示为an+1-an=d。


等差数列的性质：

（1）若公差d＞0，则为递增等差数列；若公差d＜0，则为递减等差数列；若公差d＝0，则为常数列；
（2）有穷等差数列中，与首末两端“等距离”的两项和相等，并且等于首末两项之和；
（3）m，n∈N*，则am＝an+(m-n)d；
（4）若s，t，p，q∈N*，且s+t=p+q，则as+at=ap+aq，其中as，at，ap，aq是数列中的项，特别地，当s+t=2p时，有as+at=2ap；
（5）若数列｛an｝，｛bn｝均是等差数列，则数列｛man+kbn｝仍为等差数列，其中m，k均为常数。
（6）
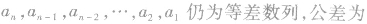
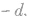
（7）从第二项开始起，每一项是与它相邻两项的等差中项，也是与它等距离的前后两项的等差中项，即
（8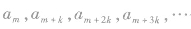） 仍为等差数列，公差为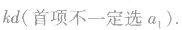


 


对等差数列定义的理解：

①如果一个数列不是从第2项起，而是从第3项或某一项起，每一项与它前一项的差是同一个常数，那么此数列不是等差数列，但可以说从第2项或某项开始是等差数列． 
②求公差d时，因为d是这个数列的后一项与前一项的差，故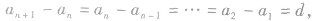有 还有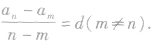
③公差d∈R，当d=0时，数列为常数列（也是等差数列）；当d>0时，数列为递增数列；当d<0时，数列为递减数列；
④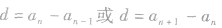 是证明或判断一个数列是否为等差数列的依据；
⑤证明一个数列是等差数列，只需证明an+1-an是一个与n无关的常数即可。

等差数列求解与证明的基本方法：

(1)学会运用函数与方程思想解题；
(2)抓住首项与公差是解决等差数列问题的关键；
(3)等差数列的通项公式、前n项和公式涉及五个量：a1，d，n，an，Sn，知道其中任意三个就可以列方程组求出另外两个(俗称“知三求二’)．


一般数列的定义：

如果数列{an}的第n项an与序号n之间的关系可以用一个式子表示成an=f（n），那么这个公式叫做这个数列的通项公式。


通项公式的求法：

（1）构造等比数列：凡是出现关于后项和前项的一次递推式都可以构造等比数列求通项公式；
（2）构造等差数列：递推式不能构造等比数列时，构造等差数列；
（3）递推：即按照后项和前项的对应规律，再往前项推写对应式。
已知递推公式求通项常见方法：
①已知a1=a,an+1=qan+b,求an时，利用待定系数法求解，其关键是确定待定系数λ，使an+1 +λ=q(an+λ)进而得到λ。
②已知a1=a,an=an-1+f(n)(n≥2),求an时，利用累加法求解，即an=a1+(a2-a1)+(a3-a2)+…+(an-an-1)的方法。
③已知a1=a,an=f(n)an-1(n≥2)，求an时，利用累乘法求解。


递增数列的定义：

一般地，一个数列{an}，如果从第2项起，每一项都大于它的前一项的数列叫做递增数列。

递减数列的定义：

如果从第2项起，每一项都小于它的前一项的数列叫做递减数列。

单调数列：

递增数列和递减数列通称为单调数列. 


数列的单调性:

1.对单调数列的理解:数列是特殊的函数,特殊在于其定义域为正整数集或它的子集.有些数列不存在单调性.有些数列在正整数集上有多个单调情况,有些数列在正整数集上单调性一定;
2.单调数列的判定方法:已知数列{an}的通项公式，要讨论这个数列的单调性，即比较an与an+1的大小关系，可以作差比较；也可以作商比较，前提条件是数列各项为正。


发现相似题
与“已知数列{an}，{bn}满足bn=an+1-an，其中n=1，2，3，…（Ⅰ）若...”考查相似的试题有：