本试题 “如图:点P在正方体ABCD﹣A1B1C1D1的面对角线BC1上运动,则下列四个命题:①三棱锥A﹣D1PC的体积不变; ②A1P∥面ACD1; ③DP⊥BC1; ④面PDB1⊥面ACD1.其中正确的命...” 主要考查您对柱体、椎体、台体的表面积与体积
空间中直线与直线的位置关系
直线与平面平行的判定与性质
平面与平面垂直的判定与性质
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 柱体、椎体、台体的表面积与体积
- 空间中直线与直线的位置关系
- 直线与平面平行的判定与性质
- 平面与平面垂直的判定与性质
侧面积和全面积的定义:
(1)侧面积的定义:把柱、锥、台的侧面沿着它们的一条侧棱或母线剪开,所得到的展开图的面积,就是空间几何体的侧面积.
(2)全面积的定义:空间几何体的侧面积与底面积的和叫做空间几何体的全面积,
柱体、锥体、台体的表面积公式(c为底面周长,h为高,h′为斜高,l为母线)
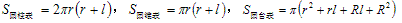
柱体、锥体、台体的体积公式:

多面体的侧面积与体积:
| 多面体 | 图像 | 侧面积 | 体积 |
| 棱柱 |
 |
直棱柱的侧面展开图是矩形 |
 |
| 棱锥 |
 |
正棱柱的侧面展开图是一些全等的等腰三角形,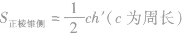 |
 |
| 棱台 |
 |
正棱台的侧面展开图是一些全等的等腰梯形,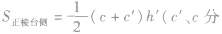  |
 |
旋转体的侧面积和体积:
| 旋转体 | 图形 | 侧面积与全面积 | 体积 |
| 圆柱 |
 |
圆柱的侧面展开图的矩形: |
 |
| 圆锥 |
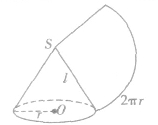 |
圆锥的侧面展开图是扇形: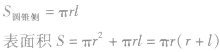 |
 |
| 圆台 |
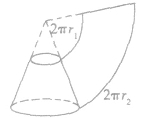 |
圆台的侧面展开图是扇环: |
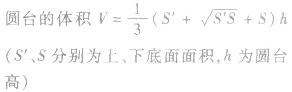 |
| 球 |
 |
 |
 |
异面直线:
不同在任何一个平面内的两条直线。
空间中直线与直线的位置关系有且只有三种 :

异面直线的判定:
过平面外一点与平面内一点的直线与平面内不过该点的直线是异面直线。
用符号语言可表示为:

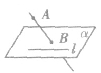
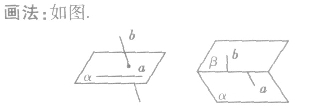
公理4:
平行于同一条直线的两条直线互相平行。
等角定理:
空间中,如果一个角的两边和另一个角的两边分别平行,那么这两角相等或互补。
异面直线的性质:
既不平行,又不相交;
证明线线平行的常用方法:
①利用定义,证两线共面且无公共点;
②利用公理4,证两线同时平行于第三条直线;
③利用线面平行的性质定理把证线线平行转化为证线面平行,转化思想在立体几何中贯穿始终,转化的途径是把空间问题转化为平面问题;
④三角形的中位线;
⑤证两线是平行四边形的对边.
线面平行的定义:
若直线和平面无公共点,则称直线和平面平行。
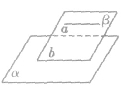
线面平行的判定定理:
平面外一条直线与此平面内一条直线平行,则该直线与此平面平行。 线线平行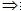 线面平行
线面平行
符号语言:
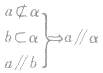
线面平行的性质定理:
如果一条直线和一个平面平行,则过这条直线的任一平面与此平面的交线与该直线平行。 线面平行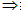 线线平行
线线平行
符号语言:
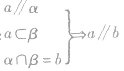
证明直线与平面平行的常用方法:
(l)反证法,即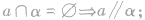
(2)判定定理法,即
(3)面面平行的性质定理,即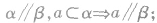
(4)向量法,平面外的直线 的方向向量n与平面
的方向向量n与平面 的法向量n垂直,则直线
的法向量n垂直,则直线 与平面
与平面 平行,即
平行,即
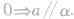
平面和平面垂直的定义:
如果两个平面相交,所成的二面角(从一条直线出发的两个半平面所组成的图形)是直二面角(平面角是直角),就说这两个平面垂直。如图,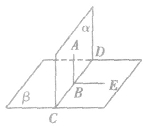
面面垂直的判定定理:
如果一个平面经过另一个平面的一条垂线,那么这两个平面互相垂直。(线面垂直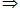 面面垂直)
面面垂直)
面面垂直的性质定理:
如果两个平面互相垂直,那么在一个平面内垂直于他们的交线的直线垂直于另一个平面。(面面垂直 线面垂直)
线面垂直)
性质定理符号表示:
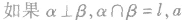

线线垂直、线面垂直、面面垂直的转化关系:
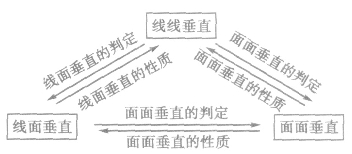
证明面面垂直的方法:
证明两个平面垂直,通常是通过证明线线垂直、线面垂直来实现的,在关于垂直问题的论证中要注意三者之间的相互转化,必要时可添加辅助线,如:已知面面垂直时,一般用性质定理,在一个平面内作出交线的垂线,使之转化为线面垂直,然后转化为线线垂直,故要熟练掌握三者之间的转化条件及常用方法.线面垂直与面面垂直最终归纳为线线垂直,证共面的两直线垂直常用勾股定理的逆定理、等腰三角形的性质;证不共面的两直线垂直通常利用线面垂直或利用空间向量.
常用结论:
(1)如果两个平面互相垂直,那么经过第一个平面内的一点垂直于第二个平面的直线在第一个平面内,此结论可以作为性质定理用,
(2)从该性质定理的条件看出:只要在其中一个平面内通过一点作另一个平面的垂线,那么这条垂线必在这个平面内,点的位置既可以在交线上,也可以不在交线上,如图.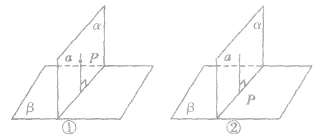
与“如图:点P在正方体ABCD﹣A1B1C1D1的面对角线BC1上运动,则下...”考查相似的试题有:
- 某几何体的三视图如图所示, 则其体积为 .
- 一个棱锥的三视图如图(尺寸的长度单位为),则该棱锥的体积是A.B.8C.4D.
- 若正三棱柱的高为3cm,连接上底面中心与下底面一边的中点的直线与底面成45°,则这个正三棱柱的体积为______cm3.
- 以下命题中错误的是( )A.如果两直线没有公共点,那么这两直线平行。B.若直线与平面没有公共点,则它们平行。C.若两平面没有...
- 分别和两条异面直线相交的两条直线的位置关系是______.
- 已知三条直线m 、n 、l 和三个平面α、β、γ,下面四个命题中正确的是[ ]A.B.C.D.
- 设m,n是平面α内的两条不同直线;l1,l2是平面β内的两条相交直线,则α∥β的一个充分而不必要条件是______.①m∥β且l1∥α ②m∥l1且...
- 如图,三角形ABC中,AC=BC=AB,ABED是边长为1的正方形,平面ABED⊥底面ABC,若G、F分别是EC、BD的中点。(Ⅰ)求证:GF//底面AB...
- 如图,在棱长为ɑ 的正方体ABCD-A1B1C1D1中,E、F、G分别是CB.CD.CC1的中点.(1)求直线 A1C与平面ABCD所成角的正弦的值;...
- 已知直角梯形ABCD中,AB∥CD,AB⊥BC,AB=1,BC=2,CD=1+3,过A作AE⊥CD,垂足为E,G,F分别为AD,CE的中点,现将△ADE沿AE折叠,...