返回

高中数学

首页
首页 高中数学知识 正弦定理 余弦定理 用数量积表示两个向量的夹角 试题正文
  • 单选题
    在△ABC中，角A，B，C的对边分别是a，b，c，下列命题：
    ①
    AB
    •
    BC
    ＞0，则△ABC为钝角三角形．
    ②若b=
    		2
    csinB，则C=45°．
    ③若a2=b2+c2-bc，则A=60°．
    ④若已知E为△ABC的边BC的中点，△ABC所在平面内有一点P，满足
    PA
    +
    PB
    +
    PC
    =0    ，设
    |
    AP
    |
    |
    PE
    |
    =λ    ，则λ=2，其中正确命题的个数是（　　）
    A．1B．2C．3D．4

    本题信息：数学单选题难度容易 来源:未知
  • 本题答案
    查看答案
本试题 “在△ABC中，角A，B，C的对边分别是a，b，c，下列命题：①AB•BC＞0，则△ABC为钝角三角形．②若b=2csinB，则C=45°．③若a2=b2+c2-bc，则A=60°．④若已知E为△ABC的边B...” 主要考查您对

正弦定理

余弦定理

用数量积表示两个向量的夹角

等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
  • 正弦定理
  • 余弦定理
  • 用数量积表示两个向量的夹角

正弦定理：

在一个三角形中，各边和它所对角的正弦的比相等，即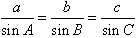=2R。
有以下一些变式：
（1）；
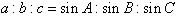（2）；
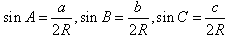（3）。


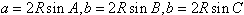正弦定理在解三角形中的应用：

（1）已知两角和一边解三角形，只有一解。
（2）已知两边和其中一边的对角，解三角形，要注意对解的个数的讨论。可按如下步骤和方法进行：先看已知角的性质和已知两边的大小关系。
如已知a，b，A，
（一）若A为钝角或直角，当b≥a时，则无解；当a≥b时，有只有一个解；
（二）若A为锐角，结合下图理解。
①若a≥b或a=bsinA，则只有一个解。
②若bsinA＜a＜b，则有两解。
③若a＜bsinA，则无解。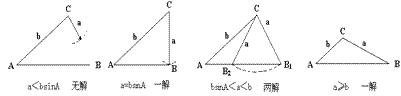

也可根据a，b的关系及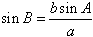与1的大小关系来确定。　　　　　　　　　



余弦定理：

三角形任意一边的平方等于其他两边的平方的和减去这两边与它们夹角的余弦的积的两倍，
即。

推论：

在△ABC中，若a2+b2=c2，则C为直角；若a2+b2＞c2，则C为锐角；若a2+b2＜c2，则C为钝角。


余弦定理在解三角形中的应用：

（1）已知两边和夹角，
（2）已知三边。


其它公式：

射影公式：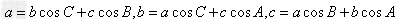


用数量积表示两个向量的夹角：

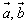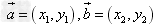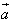设都是非零向量，，θ是与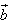的夹角，根据向量数量积的定义及坐标表示可得
。


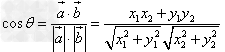向量数量积问题中方法提炼：

（1）平面向量的数量积的运算有两种形式，一是依据定义来计算，二是利用坐标来计算，具体应用哪种形式应根据已知条件的特征来选择；
（2）平面向量数量积的计算类似于多项式的运算，解题中要注意多项式运算方法的运用；
（3）平面向量数量积的计算中要注意平面向量基本定理的应用，选择合适的基底，以简化运算
（4）向量的数量积是一个数而不是一个向量。


发现相似题
与“在△ABC中，角A，B，C的对边分别是a，b，c，下列命题：①AB•BC...”考查相似的试题有：