已知cos（α+β）=13，cos（α-β）=12，则log5(tanαtanβ)=______．,高中,数学试题,对数函数的图象与性质考点,同角三角函数的基本关系式考点,两角和与差的三角函数及三角恒等变换考点,好技网

本试题 “已知cos（α+β）=13，cos（α-β）=12，则log5(tanαtanβ)=______．” 主要考查您对
对数函数的图象与性质

同角三角函数的基本关系式

两角和与差的三角函数及三角恒等变换
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。

对数函数的图形：

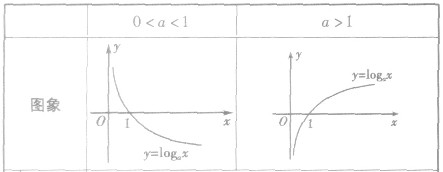
对数函数的图象与性质：

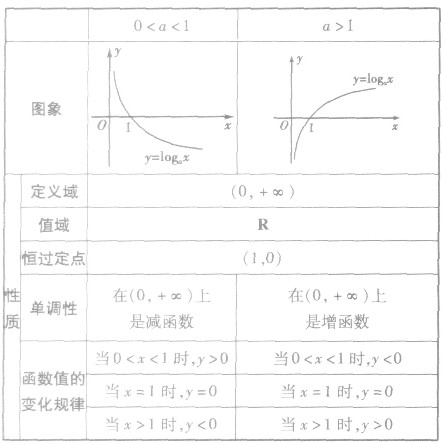
对数函数与指数函数的对比：

(1)对数函数与指数函数互为反函数，它们的定义域、值域互换，图象关于直线y=x对称．
(2)它们都是单调函数，都不具有奇偶性．当a>l时，它们是增函数；当O<a<l时，它们是减函数．
(3)指数函数与对数函数的联系与区别：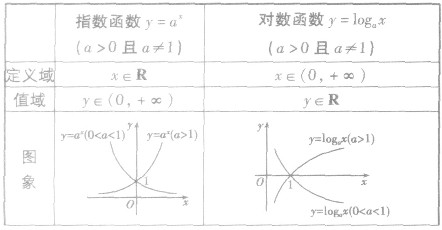

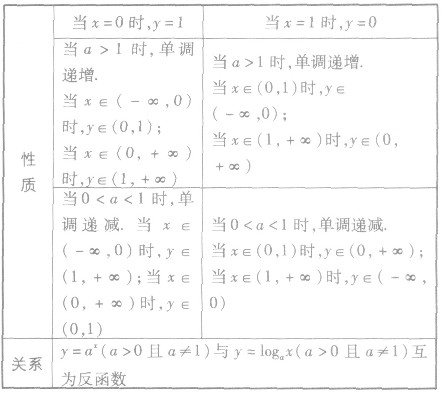
对数函数单调性的讨论：

解决与对数函数有关的函数单调性问题的关键：一是看底数是否大于l，当底数未明确给出时，则应对底数a是否大于1进行讨论；二是运用复合法来判断其单调性，但应注意中间变量的取值范围；三要注意其定义域（这是一个隐形陷阱），也就是要坚持“定义域优先”的原则．

利用对数函数的图象解题：

涉及对数型函数的图象时，一般从最基本的对数函数的图象人手，通过平移、伸缩、对称变换得到对数型函数的图象，特别地，要注意底数a>l与O<a<l的两种不同情况，

底数对函数值大小的影响：

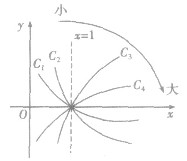
1.在同一坐标系中分别作出函数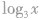的图象，如图所示，可以看出：当a>l时，底数越大，图象越靠近x轴，同理，当O<a<l时，底数越小，函数图象越靠近x轴．利用这一规律，我们可以解决真数相同、对数不等时判断底数大小的问题．

2.类似地，在同一坐标系中分别作出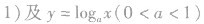的图象，如图所示，它们的图象在第一象限的规律是：直线x=l把第一象限分成两个区域，每个区域里对数函数的底数都是由右向左逐渐减小，比如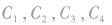分别对应函数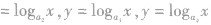，则必有

同角三角函数的关系式：

（1）；
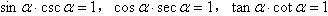（2）商数关系：；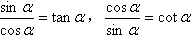
（3）平方关系：。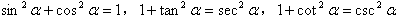

同角三角函数的基本关系的应用：

已知一个角的一种三角函数值，根据角的终边的位置利用同角三角函数的基本关系，可以求出这个角的其他三角函数值．

同角三角函数的基本关系的理解：

(1)在公式中，要求是同一个角，如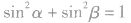不一定成立．
(2)上面的关系式都是对使它的两边具有意义的那些角而言的，如：基本三角关系式。对一切α∈R成立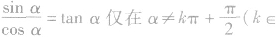； Z)时成立．
(3)同角三角函数的基本关系的应用极为为广泛，它们还有如下等价形式：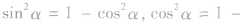

(4)在应用平方关系时，常用到平方根、算术平方根和绝对值的概念，应注意“±”的选取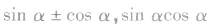．间的基本变形三者通过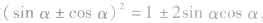，可知一求二，有关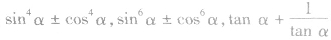等化简都与此基本变形有广泛的联系，要熟练掌握。

两角和与差的公式：

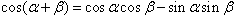
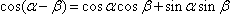
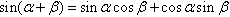
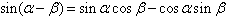
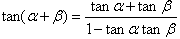
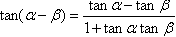
倍角公式：

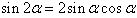
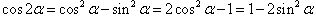
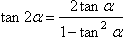
半角公式：

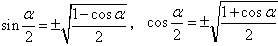
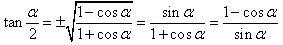
万能公式：

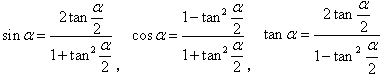
三角函数的积化和差与和差化积：

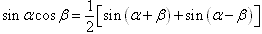
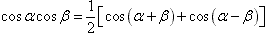
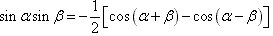
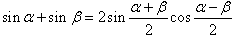
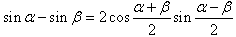
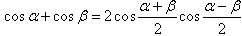
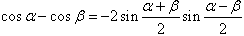
三角恒等变换：

寻找式子所包含的各个角之间的联系，并以此为依据选择可以联系它们的适当公式，这是三角恒等变换的特点。

三角函数式化简要遵循的"三看"原则:

(1)一看"角".这是最重要的一点,通过角之间的关系,把角进行合理拆分与拼凑,从而正确使用公式.
(2)二看"函数名称".看函数名称之间的差异,从而确定使用的公式.
(3)三看"结构特征".分析结构特征,可以帮助我们找到变形得方向,常见的有"遇到分式要通分"等.

方法提炼:

(1)解决给值求值问题的一般思路:
①先化简需求值得式子;②观察已知条件与所求值的式子之间的联系(从三角函数名及角入手);③将已知条件代入所求式子,化简求值.
(2)解决给值求角问题的一般步骤:
①求出角的某一个三角函数值;②确定角的范围;③根据角的范围确定所求的角.

发现相似题

与“已知cos（α+β）=13，cos（α-β）=12，则log5(tanαtanβ)=______．”考查相似的试题有：