本试题 “设实数数列{an}的前n项和Sn满足Sn+1=an+1Sn(n∈ N*)。(1)若a1,S2,-2a2成等比数列,求S2和a3;(2)求证:对k≥3有0≤ak+1≤ak≤。” 主要考查您对等比中项
一般数列的项
综合法与分析法证明不等式
反证法与放缩法
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 等比中项
- 一般数列的项
- 综合法与分析法证明不等式
- 反证法与放缩法
等比中项:
若数a,G,b成等比数列,那么就称G为a与b的等比中项,从而有G2=ab或G=±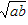 。
。
等比中项的理解:
如果a,G,b三个数成等比数列,则有G2=ab.反之不一定成立.由等比中项定义可知: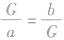 ,
, 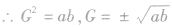 ,
,
这表明,只有同号的两项才有等比中项,并且这两项有2个互为相反数的等比中项,当a>0,b>0时,G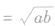 又叫做a,b的几何平均数。
又叫做a,b的几何平均数。
一般数列的项的定义:
数列中的每一个数叫做这个数列的项。
数列项的性质:
①数列的项具有有序性,一个数列不仅与构成数列的“数”有关,而且与这些数的排列顺序有关,注意与集合中元素的无序性区分开来,;
②数列的项具有可重复性,数列中的数可重复出现,这也要与集合中元素的互异性区分开来:
③注意an与{an}的区别:an表示数列{an}的第n 项,而{an}表示数列a1,a2,…,an,…,
方法提炼:
1.数列最大项、最小项、数列有界性问题可借助数列的单调性来解决,判断单调性时常用(1)作差法;(2)作差法;(3)结合函数图像等方法;
2.若求最大项an,则an满足an≥an+1且an≥an-1;若求最小项an,则an满足an≤an+1且an≤an-1。
综合法:
利用某些已知的不等式或已证过的不等式或不等式的性质推导出所要证的不等式成立,这种证明方法叫综合法,即由因导果。利用均值不等式的有关公式最为常见。
分析法:
(1)从求证的不等式出发,分析使这个不等式成立的充分条件,把证明这个不等式的问题转化为这些条件是否具备的问题,如果能肯定这些条件都已具备,那么就可以判定所证的不等式成立,这种证明方法叫分析法,即执果索因;
(2)用分析法证明要注意格式:“若A成立,则B成立”的模式是:欲证B为真,只需证C为真,只需证D为真…最后得出A或已知的性质、公理、定理,从而得出B为真。也可使用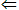 简化叙述。即B
简化叙述。即B C
C D
D …
… A或已知的性质、公理、定理。切不可使用B
A或已知的性质、公理、定理。切不可使用B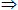 C
C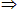 D
D …
…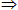 A。
A。
用综合法分析法证明不等式常用到的结论:

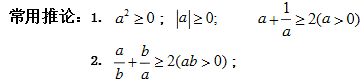
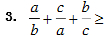 3,
3,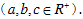
反证法的定义:
有些不等式无法利用题设的已知条件直接证明,我们可以用间接的方法——反证法去证明,即通过否定原结论——导出矛盾——从而达到肯定原结论的目的。
放缩法的定义:
把原不等式放大或缩小成一个恰好可以化简的形式,比较常用的方法是把分母或分子适当放大或缩小(减去或加上一个正数)使不等式简化易证。
反证法证题的步骤:
若A成立,求证B成立。
共分三步:
(1)提出与结论相反的假设;如负数的反面是非负数,正数的反面是非正数即0和负数;
(2)从假设出发,经过推理,得出矛盾;(必须由假设出发进行推理否则不是反证法或证错);
(3)由矛盾判定假设不正确,从而肯定命题的结论正确.矛盾:与定义、公理、定理、公式、性质等一切已有的结论矛盾甚至自相矛盾。
反证法是一种间接证明命题的基本方法。在证明一个数学命题时,如果运用直接证明法比较困难或难以证明时,可运用反证法进行证明。
放缩法的意义:
放缩法理论依据是不等式的传递性:若,a<b,b<c,则a<c.
放缩法的操作:
若求证P<Q,先证P<P1<P2<…<Pn,再证恰有Pn<Q.
需注意:(1)只有同方向才可以放缩,反方向不可。
(2)不能放(缩)得太大(小),否则不会有最后的Pn<Q.
与“设实数数列{an}的前n项和Sn满足Sn+1=an+1Sn(n∈ N*)。(1)...”考查相似的试题有:
- 已知数列的通项公式是=,则220是这个数列的[ ]A.第19项B.第20项C.第21项D.第22项
- 已知等比数列{an}的前n项和为An=2n+1-a,数列{bn}(bn>0)的首项为b1=a,且前n项和为Sn满足4Sn=bn(bn+2)(n≥2),(1)求...
- 已知数列{an},其中a2=6,且,(Ⅰ)求a1;(Ⅱ)求证:对任意n∈N*,an=n(2n-1)。
- 对于,将n表示为,当时,当时为0或1,定义如下:在n的上述表示中,当,a2,…,ak中等于1的个数为奇数时,bn=1;否则bn=0。(1...
- (1)解不等式2x2-4x-1x2-2x-3≥3;(2)a,b∈R+,2c>a+b,求证c-c2-ab<a<c+c2-ab.
- 设b>0,数列{an}满足a1=b,(n≥2)。(1)求数列{an}的通项公式;(2)证明:对于一切正整数n,2an≤bn+1+1。
- 已知:-1<b<0,a<0,那么下列不等式成立的是( ) A.a>ab>ab2 B.ab2>ab>a C.ab>a>ab2 D.ab>ab2>a
- 用反证法证明:“方程ax2+bx+c=0,且a,b,c都是奇数,则方程没有整数根”正确的假设是方程存在实数根x0为( ) A.整数 B.奇...
- (本小题满分12分)设,求证:.
- (1)已知函数f(x)=lnx-x+1,x∈(0,+∞),求函数f(x)的最大值;(2)设ak,bk(k=1,2,…,n)均为正数,证明:①若a1b1+a2b2+…+anbn≤...